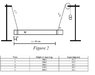
john560
- 6
- 0
Homework Statement
B. Torque Due to Perpendicular
Component of F
4. The tension in string 1 (on the left) is not
known, so we will calculate the torques
about this point (10.0 cm). (That way,
there is no torque due to the unknown
string 1.) Calculate the torque due to the
weight of the meter stick about 10.0 cm.
5. Calculate the perpendicular component
of the tension in string two (T2sinθ) for
the five different values of θ. Is the
perpendicular component of the tension
the same for each trial? Calculate the
torques due to string 2 about x = 10.0
cm. Is the net torque acting on the
meterstick about 10.0 cm equal to zero
for each trial?
Mass of meter stick= 149g
Clamps(these are the things that connect the string to the meter stick) = 17g
right side weight = 200g
left side clamp at 10.0cm
Center of mass of ruler = 50cm
right side clamp at 90 cm
Homework Equations
t= fl = rfsin(\theta) = Ftanr
The Attempt at a Solution
Calculate the torque due to the
weight of the meter stick about 10.0 cm.
4. The center of mass of the meter stick was 50 cm
So the only thing that is torquing it is the gravity of the meter stick, from the 10cm point
The weight of the meter stick(including 2 clamps = 1.79N
t= rfsin(90) \ t= (.40m) (1.792 N) (sin(90))
\ t= .717NM
Negative 717NM since the torque is clockwise
Can someone confirm that I am doing this correctly?5. I am just going to do the calculations for trail 1 to see if i am doing it correct Calculate perpendicular component of tension in string 2
\ t2sin = opposite
\ (1.98N) sin 31 = 1.02 NCalculate the torques due to string 2 about x = 10.0 cm.
t= Ftanr
\ t= (1.02 N) (.80 m)
\ t= .816 NM
Positive since torque is counterclockwise.
Calculate the torque due to the
weight of the meter stick about 10.0 cm.
For this step i just added the string 2 torque from the torque measured in 4.
net torque = .-717NM + .816NM = .099
Can someone check if i did this correctly?
Attachments
Last edited: