How Do You Determine the Mapping Functions in a Curvilinear Coordinate System?

[zaki]

Hello,

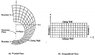
the physical domain in the (y, z) space is mapped to a rectangular computational region in the (ŋ,Ƹ)-space, where (ŋ,Ƹ) are the new coordinates. This technique frees the computational simulation from geometry restriction.

after transforming the governing equations ( PDEs) to the (ŋ,Ƹ)-space, i found a problem: i need to get the mapping relating (y,z) to (ŋ,Ƹ) because the derivatives of (y,z) with respect to (ŋ,Ƹ) appear in the transformed PDEs, in other words i need the functions:
ŋ=ŋ(y,z) and Ƹ=Ƹ(y,z)

the geometry is shown in the picture.
can anyone help me finding these functions?

 

[anuttarasammyak]

Do you have equations for lines $\eta=const.$ and $\zeta=const.$ with parameters y and z ?

 

[soloenergy]

Hi there,

It sounds like you are working with a transformation technique called "mapping" to solve your PDEs. I'm not an expert in this area, but I can try to offer some suggestions.

Firstly, have you tried looking at the literature or research papers on this technique? Sometimes, the mapping functions (ŋ and Ƹ) are already defined and used in previous studies. You can also try reaching out to the authors of these papers for more information.

If that doesn't work, you could try using a numerical method to approximate the mapping functions. This involves dividing your (y,z) space into a grid and solving for the values of ŋ and Ƹ at each grid point. This may not be the most accurate method, but it could give you a good starting point.

Another option is to use a computer program or software that specializes in mapping techniques. These programs often have built-in functions for calculating the mapping functions for different geometries.

I hope this helps. Good luck with your research!