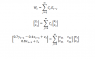How Do You Solve This Moving Average Representation Problem in Time Series?

[Kinetica]

Hi everyone!
I really need your help if you are good in time series. I have a problem on moving average representations. I attach the problem description; also, I attach my attempt to solve it. Cannot go any further. Please please help me.
Thank you!

 

[Stephen Tashi]

W_t = \begin{bmatrix} .7 & -.4 \\ .8 & 0 \end{bmatrix} \begin{bmatrix} y_{t-1} \\ x_{t-1} \end{bmatrix} + \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} e_t \\ z_t \end{bmatrix}

W_t = \begin{bmatrix} .7 & -.4 \\ .8 & 0 \end{bmatrix}\big{(} \begin{bmatrix} .7 & -.4 \\ .8 & 0 \end{bmatrix} \begin{bmatrix} y_{t-2} \\ x_{t-2} \end{bmatrix} + \begin{bmatrix} e_{t-1} \\ z_{t-1} \end{bmatrix} \big{)} +\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} e_t \\ z_t \end{bmatrix}

W_t = \begin{bmatrix} .7 & -.4 \\ .8 & 0 \end{bmatrix} \begin{bmatrix} .7 & -.4 \\ .8 & 0 \end{bmatrix} \begin{bmatrix} y_{t-2} \\ x_{t-2} \end{bmatrix} + \begin{bmatrix} .7 & -.4 \\ .8 & 0 \end{bmatrix} \begin{bmatrix} e_{t-1} \\ z_{t-1} \end{bmatrix} +\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} e_t \\ z_t \end{bmatrix}

So C_0 = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}
and C_1 = \begin{bmatrix} .7 & -.4 \\ .8 & 0 \end{bmatrix}