Linus Pauling
- 187
- 0
1.
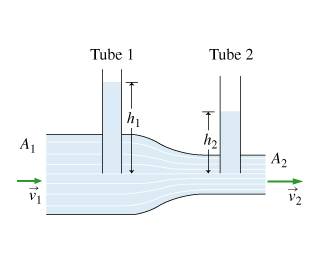
Find , the speed of the fluid in the left end of the main pipe.
Express your answer in terms of h_1, h_2 , g , A_1, A_2.
2. Bernoulli and continuity equations
3.
p_1 = rho*gh_1
p_2 = rho*gh_2
p_2 = p_1 + 0.5rho*v_1^2 + 0.5rho*(A_1/A_2)^2 * v_1^2
I know those are correct.
Substituting for p_1 and p_2, and solving for v_1 I obtain:
2g(h_2 - h_1) / [1-(A_1/A_2)]
all that under a square root.
No idea why I am getting it wrong. Should h_2 - h_1 just be h??
Find , the speed of the fluid in the left end of the main pipe.
Express your answer in terms of h_1, h_2 , g , A_1, A_2.
2. Bernoulli and continuity equations
3.
p_1 = rho*gh_1
p_2 = rho*gh_2
p_2 = p_1 + 0.5rho*v_1^2 + 0.5rho*(A_1/A_2)^2 * v_1^2
I know those are correct.
Substituting for p_1 and p_2, and solving for v_1 I obtain:
2g(h_2 - h_1) / [1-(A_1/A_2)]
all that under a square root.
No idea why I am getting it wrong. Should h_2 - h_1 just be h??