Gradon
- 3
- 0
Accelerometer Design: You have been asked to help design an accelerometer with a measurement bandwidth of 1000 Hz using a cantilevered design (see figure). The cantilever (c) has a rectangular cross-section and the proof-mass (m) is 1 gram. The cantilever can be made from single-crystal Silicon [E=190 GPa, ρ =2.3 g/cm3] or Aluminum [E = 75 GPa, ρ =2.7 g/cm3], your choice.
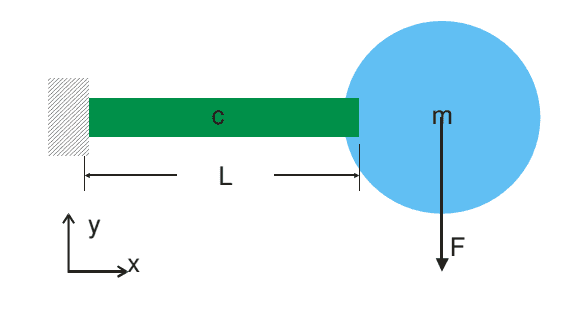
Assuming this accelerometer design can be properly modeled and analyzed as a second order system (i.e., a lumped mass-spring-damper, ignoring the mass of the cantilever), please answer the following:
a) What is the amount of stiffness in the spring element such that the natural frequency of the device is 2 kHz. Is this a good natural frequency for an accelerometer that may be used for accelerations of frequencies up to 1 kHz?
b) Please design the dimensions of the accelerometer cantilever given the stiffness calculated in part (a) such that the mass of the beam is less than 2% of the proof-mass. Also comment on which material (Silicon or Aluminum) you selected and explain why you selected this material. [Hints: This is a design problem so there are multiple solutions. If you want a more specific (constrained) case, consider a square cantilever cross-section. Recall that the deflection of a cantilever can be modeled as a linear spring and watch your units].
c) How much deflection will your designed accelerometer cantilever see subjected to a 10g acceleration (g = 9.8 m/s2) resulting from an external force (F) (assume that the cantilever is massless)?
d) Assume the requirements are that the settling time of accelerometer must be less than 20 milliseconds, what is the amount of viscous damping (or damping ratio) needed? [Hint: Assume the accelerometer is underdamped]
solve:
a.
For a cantilevered beam, the 1st natural Frep is
where B=pi/2, L=length of cantlevered, E young's moduler, I=b.h^3/12,
b. i don't know
c. deflection at beam delta=M.L/2EF
d. i don't know
can you help me to solve and edit my answer?
Assuming this accelerometer design can be properly modeled and analyzed as a second order system (i.e., a lumped mass-spring-damper, ignoring the mass of the cantilever), please answer the following:
a) What is the amount of stiffness in the spring element such that the natural frequency of the device is 2 kHz. Is this a good natural frequency for an accelerometer that may be used for accelerations of frequencies up to 1 kHz?
b) Please design the dimensions of the accelerometer cantilever given the stiffness calculated in part (a) such that the mass of the beam is less than 2% of the proof-mass. Also comment on which material (Silicon or Aluminum) you selected and explain why you selected this material. [Hints: This is a design problem so there are multiple solutions. If you want a more specific (constrained) case, consider a square cantilever cross-section. Recall that the deflection of a cantilever can be modeled as a linear spring and watch your units].
c) How much deflection will your designed accelerometer cantilever see subjected to a 10g acceleration (g = 9.8 m/s2) resulting from an external force (F) (assume that the cantilever is massless)?
d) Assume the requirements are that the settling time of accelerometer must be less than 20 milliseconds, what is the amount of viscous damping (or damping ratio) needed? [Hint: Assume the accelerometer is underdamped]
solve:
a.
For a cantilevered beam, the 1st natural Frep is
where B=pi/2, L=length of cantlevered, E young's moduler, I=b.h^3/12,
b. i don't know
c. deflection at beam delta=M.L/2EF
d. i don't know
can you help me to solve and edit my answer?
Attachments
Last edited:
![HW 5b - sensors [Compatibility Mode] - Word_2.jpg](/data/attachments/69/69422-4d167b4eae603702cd408becc53f8021.jpg?hash=TRZ7Tq5gNw)