varunKanpur
- 7
- 0
I am not able to solve this problem
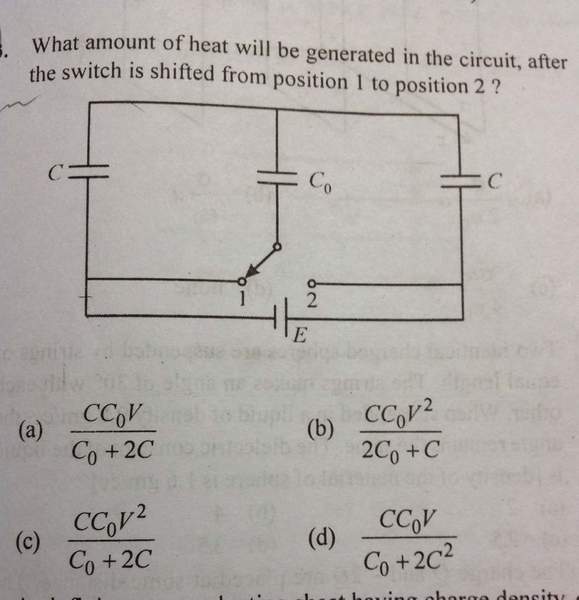
I am thinking that Co would be charging in reverse polarity switch is shifted to 2 position, so change in energy of capacitor will be released as heat energy, i.e twice the energy of stored capacitor.
I am thinking that Co would be charging in reverse polarity switch is shifted to 2 position, so change in energy of capacitor will be released as heat energy, i.e twice the energy of stored capacitor.