ellipsis
- 158
- 24
Consider a realistic pendulum with a bob of mass ##M## and a rod of mass ##m##. For the purposes of torque, is it correct to treat the bob and rod as two separate point masses, one at length ##L##, and the other at length ##\frac{L}{2}##?
When I implemented this idea, I found that centripetal acceleration increased by a factor of ##\frac{3}{2}##
The only change I detected was that the center of mass of the bob/rod combo shifted closer to the pivot, which increased the frequency of motion. In this case, the total mass had no effect.
This is the force analysis I used for a massless pendulum. For the massive pendulum, I treated the rod as a second point mass at length ##\frac{L}{2}, with its own set of forces. I then added the forces together. The acceleration due to gravity did not change (the bottom blue line), but the centripetal acceleration increased (the top blue line).
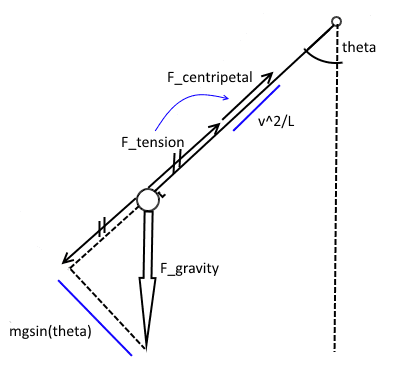
I did not specify any density information, and the pendulum swings faster, but independently of the added mass, which leads me to conclude that this is a spurious result.
If so, how should you model a pendulum with a massive rod? I'd prefer a purely force-based model (rather than Lagrangians, which I've never been introduced to)
When I implemented this idea, I found that centripetal acceleration increased by a factor of ##\frac{3}{2}##
The only change I detected was that the center of mass of the bob/rod combo shifted closer to the pivot, which increased the frequency of motion. In this case, the total mass had no effect.
This is the force analysis I used for a massless pendulum. For the massive pendulum, I treated the rod as a second point mass at length ##\frac{L}{2}, with its own set of forces. I then added the forces together. The acceleration due to gravity did not change (the bottom blue line), but the centripetal acceleration increased (the top blue line).
I did not specify any density information, and the pendulum swings faster, but independently of the added mass, which leads me to conclude that this is a spurious result.
If so, how should you model a pendulum with a massive rod? I'd prefer a purely force-based model (rather than Lagrangians, which I've never been introduced to)