ac7597
- 126
- 6
- Homework Statement
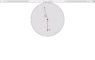
- Fred makes a circular disk of copper, with mass m=1.1 kg and radius R=0.96 meters. He drills a hole at the spot marked "X", which is 0.75 of the way from the center to the edge of the disk. He then suspends the disk from a nail, so that the disk is free to rotate around the nail.
What is the moment of inertia of the disk around the nail?
Fred now swings the disk by a small angle of θ=9.8 degrees, as shown in the diagram below. He holds the disk in this position.
What is the angular displacement from its original position? Provide the answer in radians, and use a positive value to mean "into the page" and a negative value to mean "out of the page."
In this position, what is the torque around the nail due to gravity? Use a positive value to mean "into the page" and a negative value to mean "out of the page."
Fred now releases the disk. It starts to swing back to its original orientation.
What is the initial angular acceleration of the disk?
- Relevant Equations
- torque= Force * radius * sin(theta)
moment of inertia= [(1/2)(1.1kg)(0.96)^2+ (1.1kg) (0.75*0.96)^2]= 1.08 kg*m^2
θ=9.8 degrees= 0.17 rad
torque= (mass*gravity) * radius * sin(theta)
radius= 0.17rad * 0.96m = 0.16m
torque= (1.1kg*9.8m/s^2) * 0.16m * sin(0.17rad) = 0.29 N*m
torque = inertia * angular acceleration
0.29N*m= 1.08 kg*m^2 * angular acceleration
angular acceleration = 0.27 rad/s^2
θ=9.8 degrees= 0.17 rad
torque= (mass*gravity) * radius * sin(theta)
radius= 0.17rad * 0.96m = 0.16m
torque= (1.1kg*9.8m/s^2) * 0.16m * sin(0.17rad) = 0.29 N*m
torque = inertia * angular acceleration
0.29N*m= 1.08 kg*m^2 * angular acceleration
angular acceleration = 0.27 rad/s^2