How does water rise along a glass plate? (surface tension question)

[Amitayas Banerjee]

So, I was studying about general properties of matter and topics like surface tension. I came across the phenomenon of water rising along a glass plate like in the picture. I looked for some mathematical interpretation of this on the internet and in some books.

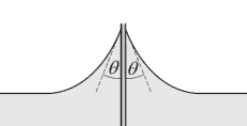
[![enter image description here][1]][1]

I looked for some mathematical interpretation of this on the internet and in some books.
I found some mathematical understanding of the phenomenon in the book **Capillarity and Wetting Phenomena: Drops, Bubbles, Pearls, Waves** and also elaborate answers on StackExchange like this one: https://physics.stackexchange.com/q...an-water-rise-above-the-edge-of-a-glass/45122

But I decided to find the height along which the water climbs on the glass by balancing forces on the **infinitely long** water element:

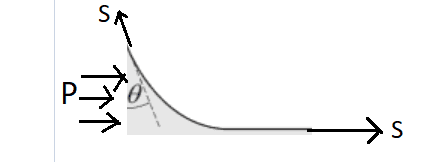
[![enter image description here][2]][2]

It is to be noted that the height of this water element is **$h$** and it has an infinite length in the horizontal direction.

Now the pressure force $P$ can be calculated as
$$P=\int_0^h \rho gz dz=\frac{1}{2}\rho g h^2 $$

On balncing forces in the horizontal direction, we get $$P+S =S\sin \theta$$ $$\Rightarrow \frac{1}{2}\rho g h^2= S(\sin \theta -1)$$ which is surely a **contradiction** as the term in the left hand side is bound to be positive. Hence I believe that I have apparently disproved the fact that water would rise along the glass plate. But I also know that this is true that water has to rise as evident from daily experiences. So, where does my math go wrong?

[1]: https://i.stack.imgur.com/FjxSP.png
[2]: https://i.stack.imgur.com/e6BNY.png

 

[Andy Resnick]

You should be balancing the vertical forces. This is a fairly standard derivation for cylindrical tubes:

https://ocw.mit.edu/courses/mathema...-2010/lecture-notes/MIT18_357F10_Lecture8.pdf

and can be carried out for planar interfaces as well:

https://tsapps.nist.gov/publication/get_pdf.cfm?pub_id=861608

 

[Chestermiller]

Your analysis is fine, except for the sign of P which should be negative rather than positive, because the pressure within the meniscus region is sub-atmospheric. The pressure increases with depth within the meniscus (from a sub-atmospheric value at the top), until it reaches atmospheric at the bottom.

If you would like me to present a detailed analysis of this straightforward problem, I can. But, again, there is nothing wrong with your assessment, aside from the sign of P.

Again, it is as simple as this: If z is the depth measured downward from the top of the meniscus, then z = h represents the horizontal surface where the gauge pressure is zero. So, within the meniscus, the gauge pressure at depth z is $-\rho g (h-z)$, so that at z = 0, the gauge pressure is $-\rho g h$.