There is an explanation of E-cube routing and a similar figure here: http://parallelcomp.uw.hu/ch02lev1sec6.html
To get from a source vertex to a destination vertex involves two operations: finding the distance between the two vertices, and then determining a path.
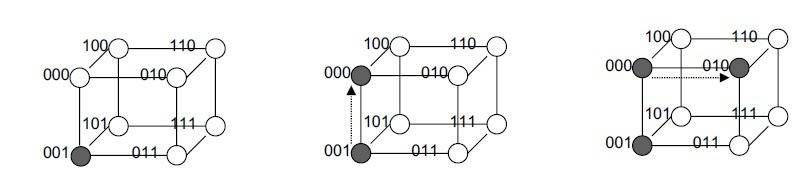
In your example, the source point, ##P_s## is at 001. The destination point, ##P_d## is at 010.
001 XOR 010 = 011, which you show. Count the number of 1 bits to get the distance, which is 2. This means that to get from one point to the other, a path of two edges has to be found.
To determine the path, the first leg will be in the direction of the least significant nonzero bit in the XOR result, 011. If you think about this bit pattern as x, y, z coordinates, in that order, the least significant bit is a 1 in the z-coordinate position, so the first leg of the path goes from 000 to 001.
The next leg of the path is determined by the 1 in the middle position of 011, which is the y-coordinate, so that leg goes from 000 to 010.
Here's a drawing of the coordinate system I'm using, based on your attached image. Your starting point is below the origin, on the z-axis. To get to the destination point, you first go to the origin, and then to the point to the right of the origin, on the y-axis.