I How find moment of inertia for car in turn?

[user079622]

I understand what is moment of inertia is, flywheel with more mass at the edge has more inertia than flywheel that has mass closer to center.

quote from link:https://decarreteres.wordpress.com/2019/04/24/chassis-engineering-polar-moment-of-inertia/

"
We will only consider the engine and gearbox as poles of inertia, since they are the elements that have the greatest influence on a vehicle. In a real calculation all the elements of the car should be taken into account.

The lengths are calculated from the vehicle’s center of gravity, to the center of gravity of each of the elements.

Let’s assume that the Porsche 904 engine in the example has a total mass of 100kg and its gearbox weighs 50kg. Also assuming that the center of gravity of the engine is 0.4m away from the center of gravity of the car, and that the gearbox is 0.8m.

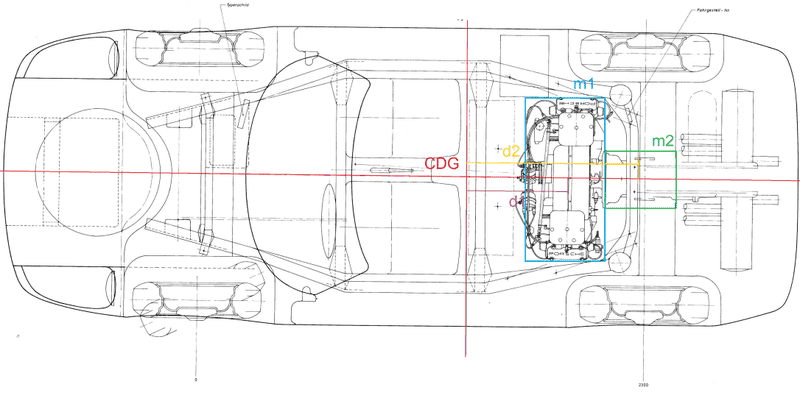
The calculation result for the Porsche 904 will be:

ΣM = m1*d1² + … + mn*dn² = 100kg *(0’4m)²+50kg*(0’8m)²= 48kgm²Let’s see now what the same calculation shows in the case of a car with it’s weights far away from the center of gravity, such as an Audi, with it’s engine ahead of the front axle.

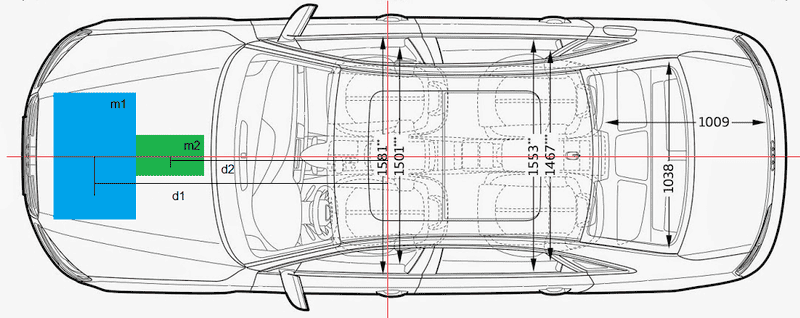
Assuming the approximate values are 100kg for the engine mass (the real one would be closer or more than 200kg), 50kg for the gearbox; The engine’s cog is at a distance of 1.5m from the center of gravity and the cog of the gearbox at 0.8m.

ΣM = m1*d1² + … + mn*dn² = 200kg *(1’5m)²+50kg*(0’8m)²= 482kgm²

After this calculation we can see that the polar moment of inertia is 10 times higher in this case, due solely to the position of the engine since the rest of the values are identical in both examples.

This means that we will need to apply 10 times more power to move the engine and gearbox in the Audi than in the Porsche. No other than the tires have the ability to do that, therefore they are suffering 10 times more load.

For this reason the vast majority of racing cars have mid engines and try to ensure that all the masses are as close as possible to the center of gravity, having as a result a very agile vehicle, even though it also means abrupt reactions.

The location of the poles of inertia influences not only the car’s nimbleness, but also the type of reactions it will have. A car will understeer if its masses are mostly in the front and will oversteer otherwise."

Why they assume that car rotate around c.g. just like seasaw rotate around fixed pivot point?
I think their pivot point is not ok..

So how to find moment of inertia for car in turn?

 

[nasu]

The moment of inertia is not an intrinsic property, like the mass. It depends on the axis taken as reference. They just calculate it around the axis passing through the center of mass. This may have several purposes. One is the the dynamics of a system is simpler if the Com is used as reference.

 

[user079622]

The moment of inertia is not an intrinsic property, like the mass. It depends on the axis taken as reference. They just calculate it around the axis passing through the center of mass. This may have several purposes. One is the the dynamics of a system is simpler if the Com is used as reference.

But you cant take axis what ever you want..?

Car front wheels turn so that mean, he "pivot" somewhere near rear axle.

If they want low moment of inertia than car "pivot" must be at c.g. that would be ideal.

 

[nasu]

You can take any axis as reference but only the one passing through the Com allows for an easy analysis of the motion. The car rotates around any axis you pick. But for any other axis the dynamic analysis is the more complex. If by "pivot" you mean the point that instantaneously at rest, this does not have to be the Com. Still, you can use the Com as reference. The car rotates around the Com, it rotates around the pivot and it rotates around any other point or axis.

 

[user079622]

You can take any axis as reference but only the one passing through the Com allows for an easy analysis of the motion. The car rotates around any axis you pick. But for any other axis the dynamic analysis is the more complex. If by "pivot" you mean the point that instantaneously at rest, this does not have to be the Com. Still, you can use the Com as reference. The car rotates around the Com, it rotates around the pivot and it rotates around any other point or axis.

What is reason why all race car have engine located in the middle(excluding porsche 911)? What that has to do with moment of inertia?

People often say 911 has engine(behind rear axle) at wrong place, why is that?

 

[nasu]

When the car goes around a curve, the motion can be seen as a linear acceleration of the center of mass and an angular acceleration around the COM. Both accelerations are due to the external forces which are applied at the wheels.
The angular acceleartion is given by $\alpha=\frac{\tau}{I}$ where $\tau$ is the torque and I is the moment of inertia. Considerind the simple model from your link, with two mases attached to a rod, if the forces are applied at the positions of the masses (these may be the wheels) the torque is proportional to the distance from the point of application and the axis (here the center). But the moment of inertia is proportional to the square of the same distance. So, if you move the masses closer to the center you decrease both the torque and the moment of inertia but the moment of inertia decreases faster and you need less force for the same acceleration. Or larger acceleration for same force, which means it turns faster in the right position. for the car is more like having this model with an extra mass along the rod. In this case the effect is even stronger because the torque does not change (forces are still applied at the wheels) but the moment of inertia decreases.

Note that this analysis does not assume that the COM is the instantaneous center of rotation at any time during the motion. It is not necessary to be so.

Also, note that I have no idea about automotive design. They may have other reasons for placing the engine where they do.

 

[user079622]

So, if you move the masses closer to the center you decrease both the torque and the moment of inertia but the moment of inertia decreases faster and you need less force for the same acceleration.

So if I want have minimum moment of inertia I must placed/design c.g. at the center(half distance between front and back wheels)?

 

[Lnewqban]

So if I want have minimum moment of inertia I must placed/design c.g. at the center(half distance between front and back wheels)?

No, as much weight as possible should be placed closer to the center of gravity.
But the yaw rotation of the car on a curve is so slow (a change of direction of 90° takes several seconds) that its rotational inertia is not very critical.

Changes in pitch and roll are much more quick, in which cases, a low moment of inertia (more weight to the center, and less to the nose and tail and sides) is beneficial to the suspension and car agility.

 

[user079622]

No, as much weight as possible should be placed closer to the center of gravity.

In both case masses are equal distance to c.g., but left case is harder to rotate becuase lever arm is longer..
So distance from c.g. to center of rotation(arm) is what affects polar moment of inertia.

I dont understand why they use c.g as pivot point?

Every object has axis where moment of inertia is smallest, so you cant choose axis what ever you want
Racket has smallest inerita at axis e1

 

[Lnewqban]

In both case masses are equal distance to c.g., but left case is harder to rotate becuase lever arm is longer..
So distance from c.g. to center of rotation(arm) is what affects polar moment of inertia.

I dont understand why they use c.g as pivot point?

Could you explain this idea a little more for me?
What are you trying to represent with your diagram?

Please, take a look at these:
http://hyperphysics.phy-astr.gsu.edu/hbase/inecon.html

http://hyperphysics.phy-astr.gsu.edu/hbase/Mechanics/angmomdem.html#c1

 

[nasu]

In both case masses are equal distance to c.g., but left case is harder to rotate becuase lever arm is longer..
So distance from c.g. to center of rotation(arm) is what affects polar moment of inertia.

I dont understand why they use c.g as pivot point?

View attachment 334182
Every object has axis where moment of inertia is smallest, so you cant choose axis what ever you want
Racket has smallest inerita at axis e1View attachment 334202

The dicussion so far assumed what is called "plane" motion (or "plane parallel"). I think that the discussion in that link assumes this situation. What this means is that when i mentioned different axes I meant that all these axes are parallel to each other and perpendicular to the plane of the motion.
If you move to the general, 3D case, the inertia is described by the tensor of inertia and not by just one number. Similar to the fact that the simple moment of inertia (for planar case) depends on the reference axis, the components of the tensor of inertia depends on the 3D coordinate system used as reference. There is a special choice of axes that makes the tensor diagonal. These are the principal axes and this is what you show in the image for the tennis racket. For this set of axes the tensor has just three non zero components. And three values for the moment of inertia. The motion is stable around either the axis with maxiumum or minimum moment of inertia. However, the principal axes are just a convenient choice not a requirement in the study of the motion. And anyway, you don't get to "choose" one of the 3 axes. If there is a general motion is in 3D, there is rotation around all 3 axes.

I don't know if this is relevant for the car motion. As @Lnewqban has mentioned, rotations about horizontal axes may happen as the car is not really a rigid body (it has suspensions). I don't see this mentioned in the OP link but I did not read it very carefully.

 

[user079622]

What are you trying to represent with your diagram?

That different axis get different moment of inertia..
I dont understand concept that you can choose whatever axis you want when anylize moment of inertia..

 

[user079622]

@nasu

You want to say if we calculate polar moment of inertia for yaw plane, that you can choose every axis you want and you will get same result?

 

[nasu]

No, the moment of inertia as well as the components of the tensor of inertia depend on the axis (axes) you choose. You can choose (in principle) any axis to analyse the motion but it does not mean you have the same moment of inertia. And the analysis of the motion is much simpler for some axis (or principal axes) than for others.

 

[Lnewqban]

That different axis get different moment of inertia..

That is correct.
But, in your post #9:
1) What are those things on the right end of the represented lever?
2) Is that hand moving?
3) Who are “they”?

I dont understand concept that you can choose whatever axis you want when anylize moment of inertia..

Please, read about parallel axis theorem in the link I have previously posted for you.

http://hyperphysics.phy-astr.gsu.edu/hbase/parax.html#pax

 

[user079622]

That is correct.
But, in your post #9:
1) What are those things on the right end of the represented lever?
2) Is that hand moving?
3) Who are “they”?Please, read about parallel axis theorem in the link I have previously posted for you.

http://hyperphysics.phy-astr.gsu.edu/hbase/parax.html#pax

1. 3 mass
2.yes hand rotate that rod,so axis of rotation is at hand, so you get correct result only if you choose axis at hand

3. People who tell that you can choose any axis

 

[user079622]

You can choose (in principle) any axis to analyse the motion but it does not mean you have the same moment of inertia.

So which axis I must choose in car case to get correct result for moment of inertia?

Further away axis is from c.g. moment of inertia is higher...but car dont have fixed pivot point (like seesaw or hand /rod in my post9) so i dont know where to put axis...

 

[nasu]

There is no such thing. For any axis you get a value which is correct for that axis.
Did you look at the parallel axis theorem suggested by @Lnewqban?

 

[user079622]

There is no such thing. For any axis you get a value which is correct for that axis.

But if car dont pivot around that axis then what is point of calculating?

 

[nasu]

What do you mean by "pivot around an axis"?

 

[user079622]

What do you mean by "pivot around an axis"?

I mean rotate around that axis

 

[nasu]

It rotates around any axis you pick. This is the point you seem to miss. There are some special axes, like the one passing through the COM and the one through the instantaneous axs of rotation, which have special properties.
But there is no axis around which the car does not rotate, if it rotates at all.
I am not sure what you mean by pivot axis. Maybe the instantaneous center? This is the point which is instanatenously at rest. It may be at one of the wheels, I don't know. But no matter where this is located, it also rotates around the COM, no matter where this is located. And this is the reference of choice for the study og the dynamics.

 

[user079622]

It rotates around any axis you pick.

But any of these axis get different moment of inertia.
So how we then find car moment of inertia?

 

[nasu]

I answered ready in post 18.

 

[user079622]

I answered ready in post 18.

That mean moment of inertia is relative ,so i can put engine/mass whatever i wont...

 

[Lnewqban]

1. 3 mass
2.yes hand rotate that rod,so axis of rotation is at hand, so you get correct result only if you choose axis at hand

3. People who tell that you can choose any axis

1) Why 3 masses?

2) But that situation is very different from the one in your original post. In real life we don't have a hand moving the car, the car is self-propelled.

3) Comparing resistance to forced rotation (about the center of mass) between both cars in the original post:

Imagine that you have a crane and sling to lift each car off the ground.
A vertical line from the hook will cross the center of mass.

You grab the nose of the Porsche and I grab the tail.
We walk in opposite directions, trying to turn the car around the hook, faster and faster (accelerated horizontal rotation).
Then, we do the same with the Audi.

Questions:
Which car offers more resistance to us?
Which car reaches a full yaw rotation quicker (while you and I are applying similar force to nose and tail of both?

 

[nasu]

That mean moment of inertia is relative ,so i can put engine/mass whatever i wont...

Yes, the moment of inertia is relative to the position of the axis. There is no doubt about this point.

The conclusion that it does not matter where you put the engine does not follow, though. There are more factors to consider, like the position of the Com relative to the points of application of external forces.

 

[user079622]

1) Why 3 masses?

Because I want point out that distance from axis of rotation(hand) to c.g. is relevenat not distance between masses and c.g.... In both case distance from masses to c.g. is the same

2) But that situation is very different from the one in your original post. In real life we don't have a hand moving the car, the car is self-propelled.

Yes I know, but how can we even talk about moment of inertia if we dont know axis of rotation!?
Like we talk about torque but we dont know what is lever arm..That dont make any sense

Which car offers more resistance to us?
Which car reaches a full yaw rotation quicker (while you and I are applying similar force to nose and tail of both?

This is case where axis of rotation("vertical axis") pass through car c.g. , harder to turn will be car that has masses further away from that axis.

Porsche has heavy engine at tail, if axis of rotation is at nose then he has big moment of inertia but if axis of rotation is at rear axle that he has very little moment of inertia because engine is close to that axis.
So my conclusion is that c.g. must as close as possible to axis of rotation, and we cant find moment of inertia if we dont know where that axis is..

Yes, the moment of inertia is relative to the position of the axis. There is no doubt about this point.

The conclusion that it does not matter where you put the engine does not follow, though. There are more factors to consider, like the position of the Com relative to the points of application of external forces.

suorce: https://www.slideserve.com/zalman/lecture-7-full-vehicle-modelling
What is this center of picture below?

 

[Lnewqban]

Pure accelerated rotation analysis should be done using cg as reference, just like it naturally happens with our crane.
You are correct, the car with heavier parts located far away from cg-axis of rotation will be much harder to rotate from repose and to stop from rotation (note that in both cases acceleration and inertia are involved).

In you diagram with the hand, we have translation of the cars, happening simultaneously with the pure rotation, which makes our analysis of moment of inertia more confusing.

Pure rotation with no translation:
Nose of car points North-you close your eyes-nose of car is pointing West when you open your eyes.
The cg has rotated over itself, but it has not moved in any direction.

Pure rotation with simultaneous translation:
Nose of car points North-you close your eyes-nose of car is pointing West when you open your eyes.
The cg has rotated over itself, like every other part of the car, and simultaneously the cg has moved describing a circular trajectory (one quarter of a circle).

In both cases, the resistance to accelerated rotation or angular inertia of the car has been exactly the same (for equal angular acceleration or $rad/s^2$).

 

[nasu]

suorce: https://www.slideserve.com/zalman/lecture-7-full-vehicle-modelling
What is this center of picture below?
View attachment 334267View attachment 334268

Some symbols are not defined in that picture but from the form of the relationship for "c" this seems to be the location of what is called "center of percution" for oscillating systems. Maybe here it will be called "center of rotation" but it is not the instantaneous center of rotation. The car seems to be rotating so that the front left wheel is the instantaneous center of rotation (possibly you will call it "pivot"). This point is at rest, its translation and rotation velocities cancel one another.
For a physical pendulum, the significance of the center of percution is that you can replace the physical pendulum with a small ball with the same mass attached to a string with the length equal to the distance between the pivot and the center of percution.

I don't know what is the importance of it for the car motion. Maybe you should reasearch this.

 

[hutchphd]

Can the OP explain what the parallel axis theorem says? I don't think so.

 

[user079622]

The car seems to be rotating so that the front left wheel is the instantaneous center of rotation (possibly you will call it "pivot"). This point is at rest, its translation and rotation velocities cancel one another.

Dont understand your view.

Center of curve is ICR not front left wheel.
Car ICR depend on acerman geometry, but that center is irrelevant for polar moment of inertia

 

[user079622]

Can the OP explain what the parallel axis theorem says? I don't think so.

Yes, for every axis that is parallel with vertical axis and perpendicular to that (in our case yaw plane) plane has moment of inertia = moment of inertia for axis that pass through c.g. + mass of object times distance^2 from c.g. to that "choosen" axis.

Also formula shows that smallest moment of inertia is when object rotate around his c.g.(axis of rotation pass through c.g)

 

[hutchphd]

So is it not obvious why one wants to know the moment of inertia about the CoM ?

 

[user079622]

So is it not obvious why one wants to know the moment of inertia about the CoM ?

If car turn front wheels 90degress to the left, and c.g. of car is in the middle, isnt obvious that axis of rotation is not pass through c.g.?

I just want to tell to find car moment of inertia we must first find out how far is axis of rotation from c.g, I bet that distance is never zero..

 

[nasu]

Dont understand your view.

Center of curve is ICR not front left wheel.
Car ICR depend on acerman geometry, but that center is irrelevant for polar moment of inertia
View attachment 334284

I did not say center of curve, did I?
Instantaneous center of rotation moves as the car moves. It's fixed just for an instant.
Do you realize that what happens here can be analized as the motion of the COM around a curved path as well as a rotation of the body around the COM? If the path of the COM is part of a circle, there is a fixed center of that path.
For the rotation around the COM, there is always an instantaneous center of rotation which is at rest at that instant. This is not the center of the curve described by the COM and may have different position on the body or outside the body, at different instants. These are basic concepts in the mechanics of rotation for rigid bodies.

 

[user079622]

Do you realize that what happens here can be analized as the motion of the COM around a curved path as well as a rotation of the body around the COM?

That implies: if COM of object move in curved path, that object can only rotate around his COM(because if not, COM will not move in curved path)

(Only when undeersteer or oversteer happend ,COM slip out from that curved path so we have complex path.)

 

[nasu]

Again, does not follow. The COM can move in a curved path no matter what. The path of the COM is determined by the external forces on the system. It is useful to consider the rotation around the COM because then the two motions can be separated (translation of COM plus rotation around the COM). This means that you can write Newton's second law separately for the two motions, you can write KE and momentum as a sum of just two terms (rotation and translation).
If he rotation is considered around any other point than COM then there are mixed terms in KE and momentum which are neither purely translation, nor purely rotation. The equatyions of motions cannot be separated anymore. Nothing wrong with this, just messy.
But the object still rotates around these not so convenient points, it does not care about how messy is our math. So when we say that "it rotates around the COM" we don't mean "it rotates only around the COM".

 

[Lnewqban]

That implies: if COM of object move in curved path, that object can only rotate around his COM(because if not, COM will not move in curved path)

(Only when undeersteer or oversteer happend ,COM slip out from that curved path so we have complex path.)

That is difficult to understand, sorry.
At high speed on a track, it will be easier to turn-in and turn-out the Porsche than the Audi, regardless the radius of the curve, or under/over steer.

The front tires of the Porsche will have less lateral force and therefore will have more grip in reserve.
The front tires of the Audi will have to apply more lateral force on the asphalt to get the car turned at the same rate, just like you and I had to apply more force on the Audi to make it spin while hanging from the crane.

As both cars should be breaking (decelerating) from the curve entry to the apex, and accelerating from the apex and out of the curve, we will have more than one type of inertia to consider.

Centralized mass is important for spinning the cars, but not for turning the cars.
Reduced total mass is important for accelerations along the curve path, but not so much for spinning the cars from North heading to West heading.

 

[user079622]

@Lnewqban

What are pros and cons of middle and rear engine position? Why people often say porsche has engine in wrong place?If engine is at rear that doesnt mean that that must be far away from c.g....

 

[Lnewqban]

@Lnewqban

What are pros and cons of middle and rear engine position? Why people often say porsche has engine in wrong place?If engine is at rear that doesnt mean that that must be far away from c.g....

That is not what the original article in post #1 explains.
It is located in the less rear position possible for a street-sport car.

 

[user079622]

I did not say center of curve, did I?
Instantaneous center of rotation moves as the car moves. It's fixed just for an instant.

So this is not ICR?

 

[user079622]

This means that you can write Newton's second law separately for the two motions, you can write KE and momentum as a sum of just two terms (rotation and translation).

Translation is tangential velocity and rotation is car spin around c.g.?

 

[nasu]

Translation means the motion of the COM, assumed to have a mass equal to the mass of the rigid object. The velocity pf the COM is always tangent to the trajectory of the COM. There is no other component. In general, velocity is tangent to the trajectory, by definition.

 

[nasu]

So this is not ICR?

View attachment 334315

It may be. Or not. How can you tell from some pictures with no context? But if they mark it as ICR it may be. It does not mean that is the same point as the center of the the trajectory described by the COM. These are distinct points in general. They may be same in some situations.

 

[user079622]

It may be. Or not. How can you tell from some pictures with no context? But if they mark it as ICR it may be. It does not mean that is the same point as the center of the the trajectory described by the COM. These are distinct points in general. They may be same in some situations.

how do you mean "with no context"?

This is center of curve, that point is at rest in space-time. Time passes but the coordinates remain the same.
Isnt it?

 

[user079622]

@Lnewqban

Does high moment of inertia drain availble tyer force so there is less for lateral direction?

 

[Lnewqban]

@Lnewqban

Does high moment of inertia drain availble tyer force so there is less for lateral direction?

Not exactly.
The lateral load trying to skid the tires is increased, but only if the car is accelerating (increasing or reducing velocity).
Therefore, there is less available traction to be used in steering and in forward acceleration or trail braking.

 

[jbriggs444]

how do you mean "with no context"?

This is center of curve, that point is at rest in space-time. Time passes but the coordinates remain the same.
Isnt it?

There is no such thing as being at rest in "space-time". Motion is always relative. Minkowski space-time offers no preferred reference frame against which to measure velocity. Nor does plain old Newtonian space-time for that matter.

The proper terminology would that the point is "at rest in our chosen frame of reference".

But which frame of reference will we choose? Probably one where the pavement is motionless. The lab frame.

But we could choose a frame of reference where the cosmic microwave background is isotropic (co-moving coordinates in cosmological terms). Then the instantaneous center of rotation could be one or two hundred kilometers away. Our drift velocity relative to the CMBR is about 369 km/sec. At a rotation rate of 0.5 radians per second, that would put the instantaneous center of rotation about 185 km away.

 

[user079622]

@jbriggs444

I understand that motion is relative term.

Flywheel rotate around center of main bearing, it is hard to me to grasp how flywheel rotate around engine mounting as well. I can't visualize that plus in reality he is not doing that...