How is the characteristic age of pulsars typically calculated?

[rnielsen25]

Hi everyone.
I'm trying to derive the formula for the characteristic age of a pulsar.

What I'm starting with is the following differential equation.
dP/dt=K*P^2-n

What i think is odd, is several places they say solving this differential equation gives the following solution.
T=(P/((n-1)*dP/dt))*(1-(P₀/P)^n-1

Here is a picture of the equation too:

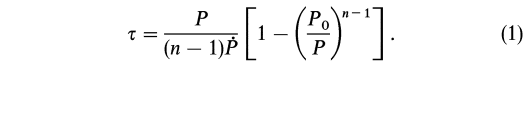
But how do you get from equation 1. to this equation.
Please help me out, if you could explain it step by step, i would really appreciate it.
Because it doesn't make sense if you're trying to separate both variables and integrate?

 

[mbond]

Hope this helps:
\dot{P}=\frac{dP}{dt}=kP^{2-n}
dt=\frac{dP}{kP^{2-n}}
\tau=t-t_{0}=\int_{P_{0}}^P \frac{dP}{kP^{2-n}}=\frac{1}{k}\frac{P^{n-1}-P_{0}^{n-1}}{n-1}=\frac{P^{n-1}}{k(n-1)}[1-(\frac{P_{0}}{P})^{n-1}]
k=\frac{\dot{P}}{P^{2-n}}
\tau=\frac{P}{(n-1)\dot{P}}[1-(\frac{P_{0}}{P})^{n-1}]

 

[Student100]

In some texts this is considered the "true" age of pulsar, although the true age would also have k and n as functions of time.

The characteristic age is typically when k is kept as constant, n = 3, and $\frac{P_0}{P} = 0$, this is an overestimation, but a decent approximation.

Have you read M&T, Pulsars?