How Long Will It Take for an Electron to Reach the Sphere's Edge?

So, in summary, the problem involves a solid dielectric sphere with a cavity of radius r and volume charge density ρ. The distance between the center of the sphere and the cavity is a. An electron is placed inside the cavity at an angle of 45° and the question is how long it will take for the electron to touch the sphere again. The electric field inside the cavity is ρa/3 directed parallel to the line joining the centers of the sphere and the cavity. However, the electric field inside the sphere will be variable, making it difficult to solve the problem.
  • #1
Tanya Sharma
1,540
135

Homework Statement



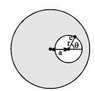
A cavity of radius r is present inside a solid dielectric sphere of radius R, having a volume charge density of ρ. The distance between the centers of the sphere and the cavity is a. An electron e is kept inside the cavity at an angle θ = 45° as shown. How long will it take to touch the sphere again?


Homework Equations





The Attempt at a Solution



The electric field inside the cavity is ρa/3 directed parallel to the line joining the centers of the sphere and the cavity ,i.e parallel to OC .

The electron is at E .So it should reach point P .After that it will enter the sphere .But the electric field will be variable inside the sphere .I am unable to proceed from here.

Not sure whether my approach is correct .

I would be grateful if somebody could help me with the problem.
 

Attachments

  • cavity.jpg
    cavity.jpg
    2.7 KB · Views: 739
  • sphere-cavity.GIF
    sphere-cavity.GIF
    3.5 KB · Views: 826
Physics news on Phys.org
  • #2
You sure they don't just want you to calculate when it hits P ?
 
  • Like
Likes 1 person
  • #3
You are right .

Thank you very much
 
Last edited:

1. What is an electron inside a cavity?

An electron inside a cavity refers to the presence of an electron in a confined space, such as a hollow cavity or container. This can occur in various scientific contexts, such as in quantum mechanics or in the study of electromagnetic radiation.

2. How does an electron behave inside a cavity?

An electron inside a cavity can behave differently depending on the specific conditions of the cavity, such as its size and shape. In general, the electron may exhibit wave-like behavior, bouncing off the walls of the cavity and creating standing waves. It may also interact with other particles or fields present in the cavity.

3. What is the significance of an electron being inside a cavity?

The presence of an electron inside a cavity can have significant implications for various scientific fields. For example, in quantum mechanics, the behavior of an electron inside a cavity can help us understand the nature of matter and energy at the atomic level. In the study of electromagnetic radiation, the presence of an electron in a cavity can influence the properties of the radiation, such as its frequency and polarization.

4. Can an electron be trapped inside a cavity?

Yes, an electron can be trapped inside a cavity under certain conditions. For example, if the walls of the cavity are reflective enough, the electron can become trapped in a standing wave pattern. Additionally, if the cavity is in a strong magnetic field, the electron's behavior may be affected and it can become trapped inside the cavity.

5. How is an electron inside a cavity relevant to technology?

The behavior of an electron inside a cavity is relevant to various technologies, such as in the development of quantum computers and the study of lasers. By understanding and manipulating the behavior of an electron inside a cavity, scientists can improve technology and create new applications in areas such as communication and computing.

Similar threads

Electric field external to Conducting Hollow Sphere with charge inside
    • Introductory Physics Homework Help
Replies
17
Views
419
Non-conductve sphere with cavity -- find Electric field
    • Introductory Physics Homework Help
Replies
7
Views
1K
Conducting sphere with chrage in centre
    • Introductory Physics Homework Help
Replies
1
Views
1K
Electric field sphere calculations with a hollow cavity using Gauss' law
    • Introductory Physics Homework Help
Replies
21
Views
2K
Center of mass of a sphere with cavity removed
    • Introductory Physics Homework Help
Replies
4
Views
7K
Electric Field in a cavity of a charged sphere
    • Introductory Physics Homework Help
Replies
11
Views
3K
A Charged Sphere with a Cavity
    • Introductory Physics Homework Help
Replies
6
Views
30K
Application of Gauss' law - point charge in hollow sphere
    • Introductory Physics Homework Help
Replies
9
Views
4K
Nonconducting spherical shell with uniform charge
    • Introductory Physics Homework Help
Replies
14
Views
12K
Solid conductor sphere with cavity inside
    • Introductory Physics Homework Help
Replies
2
Views
2K

Hot Threads

Recent Insights

Back
Top