We have two cases to consider here, one is when $x+9\ge 0$ and the other is when $x+9< 0$.If $x+9\ge 0$ (i.e. $x \ge -9$), then the inequality becomes
$$||x+9-18|-98| \le 82$$
$$||x-9|-98| \le 82$$
[TABLE="class: grid, width: 500"]
[TR]
[TD]i.[/TD]
[TD]ii.[/TD]
[/TR]
[TR]
[TD]Now, let $x-9\ge 0$ (i.e. $x \ge 9$), we have[/TD]
[TD]Now, let $x-9< 0$ (i.e. $x \ge 9$), we have[/TD]
[/TR]
[TR]
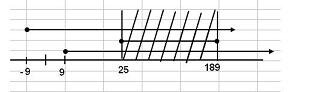
[TD]$$|x-9-98| \le 82$$
$$|x-107| \le 82$$
$$-82 \le x-107 \le 82$$
$$25 \le x \le 189$$[/TD]
[TD]$$|-(x-9)-98| \le 82$$
$$|-x-89| \le 82$$
$$-82 \le -x-89 \le 82$$
$$-171\le x \le -7$$[/TD]
[/TR]
[TR]
[TD]
View attachment 1395
The number of integers that satisfy the aforementioned relation is thus $165$.[/TD]
[TD]
View attachment 1396
The number of integers that satisfy the aforementioned relation in this particular case is thus $2$.[/TD]
[/TR]
[/TABLE]
But if $x+9< 0$ (i.e. $x<-9$), then the inequality becomes
$$||-x-9-18|-98| \le 82$$
$$||-x-27|-98| \le 82$$
[TABLE="class: grid, width: 500"]
[TR]
[TD]i.[/TD]
[TD]ii.[/TD]
[/TR]
[TR]
[TD]Now, let $-x-27\ge 0$, we have[/TD]
[TD]Now, let $-x-27< 0$, we have[/TD]
[/TR]
[TR]
[TD]$$|-x-27-98| \le 82$$
$$|-x-125| \le 82$$
$$-207 \le x \le -43$$[/TD]
[TD]$$|-(-x-27)-98| \le 82$$
$$|x-71| \le 82$$
$$-11\le x \le 153$$[/TD]
[/TR]
[TR]
[TD]The number of integers that satisfy the aforementioned relation is thus $165$.[/TD]
[TD]The number of integers that satisfy the aforementioned relation in this particular case is thus $2$.[/TD]
[/TR]
[/TABLE]
Therefore, the total number of integers satisfy the relation $$|||x+9|-18|-98| \le 82$$ is $165+3+165+2=335$.
Hey
kaliprasad, I'm sorry because according to my previous reply, I told you the answer that I've gotten was 332, which isn't the correct answer.