~angel~
- 150
- 0
Please help.
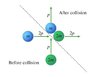
Two particles move perpendicular to each other until they collide. View Figure Particle 1 has mass m and momentum of magnitude 2p, and particle 2 has mass 2m and momentum of magnitude p. Note: Magnitudes are not drawn to scale in any of the figures.
a. Suppose that after the collision, the particles "trade" their momenta, as shown in the figure. That is, particle 1 now has magnitude of momentum p, and particle 2 has magnitude of momentum 2p; furthermore, each particle is now moving in the direction in which the other had been moving. How much kinetic energy, K_lost, is lost in the collision?
b.Consider an alternative situation: This time the particles collide completely inelastically. How much kinetic energy K_lost is lost in this case?
I've already found the answer to part a, which is 3p^2/4m, and as I was trying to work out the answer to b, I ended up with the asme answer, and I followed all the "instructions" in my textbook. Please help.
Two particles move perpendicular to each other until they collide. View Figure Particle 1 has mass m and momentum of magnitude 2p, and particle 2 has mass 2m and momentum of magnitude p. Note: Magnitudes are not drawn to scale in any of the figures.
a. Suppose that after the collision, the particles "trade" their momenta, as shown in the figure. That is, particle 1 now has magnitude of momentum p, and particle 2 has magnitude of momentum 2p; furthermore, each particle is now moving in the direction in which the other had been moving. How much kinetic energy, K_lost, is lost in the collision?
b.Consider an alternative situation: This time the particles collide completely inelastically. How much kinetic energy K_lost is lost in this case?
I've already found the answer to part a, which is 3p^2/4m, and as I was trying to work out the answer to b, I ended up with the asme answer, and I followed all the "instructions" in my textbook. Please help.