I How things appear to an accelerated observer

[Freixas]

I've been working on a Minkowsky spacetime diagram generator. The software is probably way overkill, but I'm retired and it keeps my brain active. I am no physicist, but I am a pretty good programmer.

Side note: if you have any interesting things to diagram on a 2D Minkowsky spacetime diagram, let me know. I need good test cases.

The software is complete enough that I can draw diagrams, but I'm still hunting for bugs. The software has the ability to define a problem with respect to one inertial frame and draw it with respect to another. It also allows for animations, and I can set up animations where every frame is drawn relative to a different inertial frame. This makes it possible to view things from the point of view of an accelerated observer in a variety of ways.

Here is a simple setup I tried. An observer accelerating at 1g travels 4 light years. At (0,0), the accelerating observer's velocity is 0. We'll call her Alice. There are two other observers, one at (0,0) (Bob)and one at (4,0) (Ted), both at rest with respect to each other and to Alice (at time 0). Here is a diagram that includes just Alice's worldline.

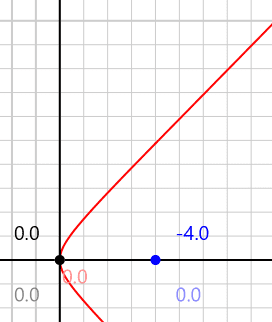The solid colors represent where Alice sees Bob (black) and Ted (blue). The solid numbers represent the times she would see if Bob and Ted displayed huge clocks and Alice had a powerful telescope. The faded colors represent the calculated position (per Alice) of Bob and Ted, and the faded numbers are their calculated clock times. For example, Alice starts out seeing Ted 4 light years away and displaying a clock time of -4.

Here is an animation of the scenario, from Alice's point of view, from time 0 until she reaches Ted.

Since we are viewing this from Alice's point of view, her position doesn't change. I believe this animation is correct, but it surprised me. As Alice accelerates toward Ted, Alice sees Ted receding into the distance—at least, until his clock reaches 0.

Let me know if this animation looks wrong and in what way.

 

[Ibix]

I'm a bit confused about what's what. The Minkowski diagram looks fine, but I'm not sure what the gif is supposed to be showing me. Are you trying to represent what Alice actually sees? If so I'm not sure it's right for the eternally accelerating observer in your Minkowski diagram since she shouldn't see the blue guy at 4ly. Or are you trying to depict the distance to the blue guy in Alice's momentarily co-moving inertial frame? That looks more plausible, although I haven't checked the maths. What are the fainter dots in the animation?

 

[Freixas]

If so I'm not sure it's right for the eternally accelerating observer in your Minkowski diagram since she shouldn't see the blue guy at 4ly.

I don't understand your question, the part about seeing "the blue guy at 4ly." The blue guy is Ted and he is always visible to Alice. At time 0, she sees Ted as 4 LY away and with a clock reading of -4 years. At Alice's time 2.2 years, she reaches Ted, who now displays a clock time of 4.9 years.

Or are you trying to depict the distance to the blue guy in Alice's momentarily co-moving inertial frame?

Exactly. Every instant in the animation is from Alice's view.

What are the fainter dots in the animation?

The fainter dots represent where Alice calculates the positions of Bob and Ted. The fainter text represents the clock times she calculates fro them.

For example, at time 0, Alice sees Ted's clock reading -4 years, but calculates his clock (along her current line of simultaneity) to read 0. At that instant, of course, her inertial frame matches Bob's and Ted's.

 

[PeterDonis]

Since we are viewing this from Alice's point of view

How are you calculating "Alice's point of view". You can't just be reading it off a Minkowski diagram, because Alice is not an inertial observer, so any coordinate chart in which Alice is at rest cannot be a Minkowski coordinate chart. What chart are you using?

 

[Ibix]

I don't understand your question, the part about seeing "the blue guy at 4ly." The blue guy is Ted and he is always visible to Alice. At time 0, she sees Ted as 4 LY

Not if she's eternally accelerating and you are talking about what she actually sees through a telescope, since she sees the past and she wasn't 4ly from Ted in the past. I think you are saying "see" when you means "calculates based on observation and prediction of what Ted has been doing since the light now arriving left him". If so, I agree about 4ly.

Exactly. Every instant in the animation is from Alice's view.

There isn't a unique frame for Alice, so she doesn't really have a "point of view" without some further specification. I thought what you are doing is calculating the interval along the line Lorentz-orthogonal to Alice's worldline between Alice and Ted, but...

The fainter dots represent where Alice calculates the positions of Bob and Ted. The fainter text represents the clock times she calculates fro them.

For example, at time 0, Alice sees Ted's clock reading -4 years, but calculates his clock (along her current line of simultaneity) to read 0. At that instant, of course, her inertial frame matches Bob's and Ted's.

...then I am confused again. Can you sketch on the Minkowski diagram or state mathematically what calculations you are doing at some arbitrary time after t=0?

 

[Freixas]

How are you calculating "Alice's point of view". You can't just be reading it off a Minkowski diagram, because Alice is not an inertial observer, so any coordinate chart in which Alice is at rest cannot be a Minkowski coordinate chart. What chart are you using?

Yes, I am using Minkowsky spacetime diagrams. Any single frame of the animation is a Minkwosky spacetime diagram using Alice's instantaneous moving frame (IMF). The IMF changes for each frame.

Unfortunately, some of the animated diagrams that make it clearer are too big to post here. I may try to post a few stills when I get a chance.

But how I do it seems irrelevant. If you were Alice, would you see Ted recede as you accelerated towards him?

 

[PeterDonis]

Any single frame of the animation is a Minkwosky spacetime diagram using Alice's instantaneous moving frame (IMF). The IMF changes for each frame.

So how are you calculating where Bob and Ted are if you're changing frames all the time?

how I do it seems irrelevant.

It most certainly is not. Wrong calculations give wrong answers. Garbage in, garbage out.

 

[PeterDonis]

If you were Alice, would you see Ted recede as you accelerated towards him?

How would Alice measure the distance to Ted? You can't just "see" someone receding. You need to have some way of measuring their distance from you.

 

[Freixas]

Not if she's eternally accelerating and you are talking about what she actually sees through a telescope, since she sees the past and she wasn't 4ly from Ted in the past. I think you are saying "see" when you means "calculates based on observation and prediction of what Ted has been doing since the light now arriving left him". If so, I agree about 4ly.

I'll try to post some diagrams to make this clearer.

But I'd ask you the same question, I asked Peter: If you were Alice, would you see Ted recede as you accelerated towards him?

 

[PeterDonis]

If you were Alice, would you see Ted recede as you accelerated towards him?

How is Ted moving? Is he stationary in the spacetime diagram you posted in your OP?

 

[Freixas]

How would Alice measure the distance to Ted? You can't just "see" someone receding. You need to have some way of measuring their distance from you.

Let's assume a super-telescope with super-precise measurements. Let's say Ted is on a very large planet and Alice knows the exact diameter of the plant. Could Alice measure the diameter of the planet as seen through the telescope and determine Ted's distance from her using only the light received by her at that point in time?

 

[PeterDonis]

The solid numbers represent the times she would see if Bob and Ted displayed huge clocks and Alice had a powerful telescope. The faded colors represent the calculated position (per Alice) of Bob and Ted, and the faded numbers are their calculated clock times.

If Alice sees Ted's clock reading -4 years in a telescope when she is at (0, 0) in your diagram, then Ted's clock does not read -4 years when he is at the point where the blue dot is in your diagram, point (4, 0) (putting the $x$ coordinate first, then the $t$ coordinate). Light travels at a finite speed. So the light Alice is seeing from Ted at (0, 0), which shows Ted's clock reading -4, was emitted by Ted at (4, -4). At (4, 0), where the blue dot is, Ted's clock will read 0.

 

[PeterDonis]

Could Alice measure the diameter of the planet as seen through the telescope and determine Ted's distance from her using only the light received by her at that point in time?

No, because light travels at a finite speed, so she is not seeing the diameter of the planet at the time she receives the light, but the diameter of the planet at the time the light was emitted.

 

[Freixas]

How is Ted moving? Is he stationary in the spacetime diagram you posted in your OP?

Bob and Ted are moving inertially. As to whether he is stationary, relative to who? Bob and Ted view each other as having a relative velocity of 0 and view Alice as accelerating.

The initial diagram I posted is for an instant in time in which everyone has a relative velocity of 0. Alice is the only one accelerating.

 

[PeterDonis]

Bob and Ted are moving inertially.

That tells me nothing about their worldlines except that they are straight lines in a Minkowski diagram. I am asking which straight lines they are in the Minkowski diagram in your OP.

As to whether he is stationary, relative to who?

I said "stationary in the spacetime diagram in your OP". That would mean Ted's worldline would be a vertical line in that diagram. Is that the case?

 

[Freixas]

No, because light travels at a finite speed, so she is not seeing the diameter of the planet at the time she receives the light, but the diameter of the planet at the time the light was emitted.

Exactly. I am asking if she can measure the apparent distance, not the actual distance, the distance that Ted appears to be at the moment the light reaches Alice.

 

[Freixas]

That would mean Ted's worldline would be a vertical line in that diagram. Is that the case?

Both Bob's and Ted's worldline would be vertical at that instant in time. Since I am viewing things from Alice's viewpoint. their worldlines remain lines, but they don't remain vertical.

 

[Ibix]

But I'd ask you the same question, I asked Peter: If you were Alice, would you see Ted recede as you accelerated towards him?

I'm struggling to understand how you are defining "see" at the moment.

In terms of Alice's proper time $\tau$ I make it that the Alice's worldline (in Ted's rest frame) is$$\begin{eqnarray*}
x&=&\frac 1a\cosh(a\tau)-\frac 1a\\
t&=&\frac 1a\sinh(a\tau)
\end{eqnarray*}$$and that simultaneously (meaning along the radius of her hyperbola) Ted's coordinates are$$\begin{eqnarray*}
x&=&L\\
t&=&\frac La\tanh(a\tau)
\end{eqnarray*}$$and that the distance between them along that line is a mess. In the case that $a=1\mathrm{ly/y^2}\approx 1g$ and $L=4\mathrm{ly}$ it simplifies to $$\sqrt{1-\frac{10}{\cosh(\tau)}+\frac{25}{\cosh^2(\tau)}}$$which is monotonically decreasing, if that helps.

Edit: missed a few posts and have to do something else now - apologies if you've already explained your definition of "see".

 

[PeterDonis]

I am asking if she can measure the apparent distance, not the actual distance, the distance that Ted appears to be at the moment the light reaches Alice.

There is no such thing because light travels at a finite speed. So the light that is reaching Alice is telling her how Ted appeared in the past, not at the moment the light reaches her.

Both Bob's and Ted's worldline would be vertical at that instant in time.

You didn't read my question carefully. I asked how Bob's and Ted's worldlines appear in the diagram you gave in the OP. That diagram is in one particular Minkowski frame. If Bob's and Ted's worldlines are vertical at any instant in that diagram, they are vertical everywhere.

Since I am viewing things from Alice's viewpoint. their worldlines remain lines, but they don't remain vertical.

Your version of "Alice's viewpoint" is not a single frame but a mishmash of frames changing at every instant, so it is meaningless to talk about the shape of any worldline in your version of "Alice's viewpoint", since there aren't even any worldlines in it, only a series of snapshots, each of a different frame at a different instant.

If you think I am implying that your version of "Alice's viewpoint" is not a good way to analyze Alice's viewpoint, you are correct.

 

[Ibix]

OK, so I think I understand what you are doing now, @Freixas. Ted emits a pulse of light which arrives at Alice at some time when she has velocity $v$ in the frame shown in the Minkowski diagram in your OP. You transform to the inertial frame with velocity $v$ (so Alice is instantaneously at rest) and calculate the distance in this frame between Alice and Ted at the times in this frame of the emission event (dark blue dot) and reception event (pale blue dot). Right?

The problem is that using an instantaneously co-moving inertial frame like that gives you inconsistent results, essentially because Alice is rewriting her history: she is always stationary now and moving in the past, and what she said a moment ago about being stationary is forgotten. We have always been stationary with respect to Eastasia, you might say. So, for example, using your method the "distance now" when Ted's clock reads zero is 4ly, but the "distance when she sees his clock reads zero" is not 4ly - it's about as far to the right as you can go in your gif. So you don't have a consistent measurement of distance because of this rewriting of history.

What you need to do is have a consistent coordinate system - Rindler coordinates work for this case, or more generally radar coordinates (https://www.mrao.cam.ac.uk/~clifford/publications/abstracts/ced_twins.html) are very useful.

 

[Freixas]

Let me re-start by re-phrasing my basic question in a way that doesn't, for the moment, involve my diagrams.

• At time 0, Alice has velocity of 0 relative to Ted.
• At time 0, Ted is 4 LY from Alice.
• At time 0, she begins accelerating at 1g toward Ted.
• At time 0, she receives an image of Ted from light that left Ted four years prior. In this image, Ted is holding a BIG ruler.

As Alice accelerates toward Ted, does Ted's ruler appear to grow bigger or smaller?

@Ibix @PeterDonis <--I'm hoping this tags my response so it notifies the two of you.

 

[Freixas]

OK, so I think I understand what you are doing now, @Freixas. Ted emits a pulse of light which arrives at Alice at some time when she has velocity in the fame in your OP. You transform to the inertial frame with velocity (so Alice is instantaneously at rest) and calculate the distance in this frame between Alice and Ted at the times of the emission event (dark blue dot) and reception event (pale blue dot). Right?

You are right about the emission event.

The pale blue dot is just the distance to Ted calculated along Alice's instantaneous line of simultaneity, the points in space which she would assign (at that moment) the same time coordinate as appears on her clock.

The problem is that using an instantaneously co-moving inertial frame like that is that you get inconsistent results,

I'll defer to you on the general principle. But bear with me. Let's say that the pale blue dot falls under your "inconsistent results" umbrella. Let's focus on the solid blue dot—it is solid because it represents something directly observed, not calculated. I cannot picture how Alice's observations can be inconsistent.

Alice receives an image from Ted where Ted is holding a BIG ruler and a BIG clock. She reads Ted's clock. She calculates Ted's distance using basic trigonometry (she knows the actual size of the ruler). None of this can be ambiguous and, at this point, I believe both can be calculated.

 

[PeterDonis]

• At time 0, Alice has velocity of 0 relative to Ted.
• At time 0, Ted is 4 LY from Alice.

Both of these claims are frame-dependent. If they are true in one frame (I assume you intend them to be true in the frame that is shown in the diagram in your OP), they will not be true in any other frame.

• At time 0, she begins accelerating at 1g toward Ted.

This could be phrased in a frame-independent way, by specifying the time on Alice's clock when she starts accelerating. In general, things that can be phrased in a frame-independent way should be, since all of the actual physics must be frame-independent.

• At time 0, she receives an image of Ted from light that left Ted four years prior.

The "four years prior" is also frame-dependent; if it is true in the frame shown in the diagram in your OP (which I assume is what you intended), it will not be true in any other frame. (Also, "at time 0" here could mean the time by Alice's clock, which would be a frame-independent way of specifying the reception event itself.)

• In this image, Ted is holding a BIG ruler.

Oriented how? Along the direction of relative motion, or perpendicular to it?

 

[PeterDonis]

Let's focus on the solid blue dot—it is solid because it represents something directly observed, not calculated.

What direct observation does the solid blue dot represent? Remember that we have already said that the distance from Ted to Alice at a given instant of time cannot be directly observed, because light has a finite speed.

 

[PeterDonis]

Alice receives an image from Ted where Ted is holding a BIG ruler and a BIG clock. She reads Ted's clock. She calculates Ted's distance using basic trigonometry (she knows the actual size of the ruler).

She can calculate a "distance" from this data, but it will not have any physical meaning, because, as I have already pointed out several times now, light travels at a finite speed.

 

[Ibix]

Let's focus on the solid blue dot—it is solid because it represents something directly observed, not calculated.

The clock measurement seen is directly observed, yes. Taking into account your question about a ruler held by Ted, the angular subtense of the ruler (I assume it's being held perpendicular to the line between them) is also directly observed. Converting any of that into a distance requires making assumptions about frames, though, and that's where you need to be careful.

 

[Freixas]

Converting any of that into a distance requires making assumptions about frames, though, and that's where you need to be careful.

Let's say that every second Alice measures the size of Ted's ruler and makes the trigonometric calculation to get a number, which may or may not represent a distance. As she accelerates toward Ted, does the value she calculate get bigger or smaller?

Or, even simpler, will Ted appear to shrink in the telescope?

 

[PeterDonis]

will Ted appear to shrink in the telescope?

This one is easy: no.

 

[Freixas]

I said I'd post some other diagrams. It's pretty easy with my tool to switch the viewpoints and change various parameters.

I've re-drawn the diagram from the point of view of Bob. I've captured three frames, at Alice's time .5, 1, and 1.5 years. I've added some features that make it harder to read, so I removed Bob's data and just focused on Alice and Ted.

The magenta axes are Alice's instantaneous moving frame's (IMF) axes. The grid is Alice's IMF's grid. The red dot is her position. The red hyperbola is her worldline.

The blue line is Ted's worldline.

The yellow line is the worldline of a photon that travels from Ted to Alice's current position. The dark blue dot is the originating event on Ted's worldline that launched the photon. The matching label gives Ted's clock time (which no one seems to get upset about) and Ted's distance from Alice (which seems to bug people because it's measured using an IMF).

The cyan line is Alice's IMF line of simultaneity, all the the coordinates in space which have the same time value relative to the IMF. The faded blue dot is where the line of simultaneity crosses Ted's worldline. The associated label gives Ted's clock time (calculated) and Ted's distance from Alice (calculated and relative to Alice's IMF).

I should also note that the grid lines on the final shot have been auto-scaled by 10 or else they would have been too dense.

I also have these same views from Alice's point of view. I had to re-scale and I dropped Bob's axes as they weren't useful and were obscuring things.

 

[jartsa]

As Alice accelerates toward Ted, does Ted's ruler appear to grow bigger or smaller?

On Alice's retina the image of the ruler gets smaller as Alice moves faster towards said ruler. So Alice could very well have an experience somewhere in her visual brain area about of a receding ruler.

I know the image gets smaller because ... it's just a basic thing about light rays.

Oh yes, we need to postulate that the ruler is so far away that Alice only travels a very small fraction of said distance during a time during which she changes her velocity quite a lot. So that only the change of velocity has an effect on the image formed on her retina, not the change of her position.

 

[PeterDonis]

I know the image gets smaller because ... it's just a basic thing about light rays.

What "basic thing about light rays" do you have in mind here?

 

[jartsa]

What "basic thing about light rays" do you have in mind here?

Relativistic beaming. Which means light rays become more parallel. Which means that a lens focuses those rays on a smaller spot.

 

[PeterDonis]

Relativistic beaming.

Ah, ok. But I'm still not sure why you added this in your earlier post:

Oh yes, we need to postulate that the ruler is so far away that Alice only travels a very small fraction of said distance during a time during which she changes her velocity quite a lot. So that only the change of velocity has an effect on the image formed on her retina, not the change of her position.

First, if the velocity is relativistic, so that beaming is significant, the change of position must also be significant; you can't make the latter small without making the former small.

Second, even if you focus on the period of initial acceleration, so that possibly the velocity change could be large before the velocity itself becomes relativistic (even though this will only be true for a limited time), for that the criterion is not that the distance to the ruler is large (at the start). It is that the proper acceleration times the distance is large, so that the distance over which the proper acceleration changes the velocity by a large amount is much smaller than the total distance to the ruler.

Unfortunately this will not be true in the scenario as given, since Alice's acceleration is 1 g, which is equivalent to about 1 inverse light-year, and Ted's initial distance from Alice (in the original rest frame, the one shown in the diagram in the OP) is 4 light years, so the product of proper acceleration and distance is only 4. Or, to put this another way, it will take about a year by Alice's clock for her speed relative to Ted to become relativistic so that beaming is significant, and by that time she will already have covered a substantial fraction of the distance to Ted.

 

[Freixas]

Or, to put this another way, it will take about a year by Alice's clock for her speed relative to Ted to become relativistic so that beaming is significant, and by that time she will already have covered a substantial fraction of the distance to Ted.

Hmm...this is interesting. I don't know what you guys are talking about, but when Alice's clock reads 1 year, she has traveled 0.6 LY in 1.2 Y rest time and has a velocity of 0.8c.

I'm using the equations at https://math.ucr.edu/home/baez/physics/Relativity/SR/Rocket/rocket.html. He has a handy little table that says that at Alice's time 1 Y, the rest time is 1.9 Y, the rest distance traveled is only .56 LY and her velocity would be 0.77c, close enough because I'm rounding. This doesn't sound like a "a substantial fraction of the distance to Ted."

 

[Freixas]

This one is easy: no.

Easy-peasy, but a one-word answer is not an explanation.

I'm willing to accept that my method of determining the distance Alice would calculate for Ted is wrong. I still believe she could calculate a distance (based on trig) and that this calculated value could be predicted knowing only the basics that I've described.

When Alice is at Bob's position, she sees what Bob sees and both should calculate the same distance based on the same trigonometry and come up with a distance of 4 LY. When Alice reaches Ted, she should easily calculate a distance of 0 LY. What is the proper method to determine the results of Alice's calculation at an arbitrary point in between?

 

[PeterDonis]

when Alice's clock reads 1 year, she has traveled 0.6 LY in 1.2 Y rest time and has a velocity of 0.8c.

These values are correct in the original rest frame, the one diagrammed in your OP. But not in any other frame.

 

[PeterDonis]

This doesn't sound like a "a substantial fraction of the distance to Ted."

It's enough of one to make the condition @jartsa gave, that the effect of the velocity change should be much greater than the effect of the position change, not valid.

 

[PeterDonis]

I don't know what you guys are talking about

Wikipedia has a decent article on it:

https://en.wikipedia.org/wiki/Relativistic_beaming

It doesn't talk much about the effect on the apparent size of objects, though. The basic idea is this: suppose we have three observers, all co-located and all looking at the same distant object. Observer A is at rest relative to the distant object; observer B is moving towards the distant object at relativistic speed; and observer C is moving away from the distant object at relativistic speed. Then the following will be true:

Compared to observer A, observer B sees the object to be brighter, to be emitting light of higher frequency, and to have a smaller apparent size.

Compared to observer A, observer C sees the object to be dimmer, to be emitting light of lower frequency, and to have a larger apparent size.

The above is what @jartsa was calling the effect due to velocity.

However, note carefully that the above is what will be true at the instant when all three observers are co-located. As observer B moves towards the distant object, its apparent size will increase because it is getting closer; and as observer C moves away from the distant object, its apparent size will decrease because it is getting further away. This is what @jartsa was calling the effect due to position, and it is opposite from the velocity effect described above.

a one-word answer is not an explanation.

In your scenario, the effect due to velocity described above will be more than counteracted by the effect due to position. To put it another way, Alice is accelerating slowly enough that the gradual decrease in Ted's apparent size due to her increasing velocity is more than counteracted by the gradual increase in Ted's apparent size due to her decreasing distance from him.

For Ted's apparent size to decrease, Alice would have to accelerate extremely hard, at billions or trillions of g's, so that her velocity became relativistic very quickly, while her distance to Ted hardly changed at all. Then, during that initial period, where her velocity was going from zero to relativistic, Ted's appparent size to her would decrease because the velocity beaming effect would be changing very rapidly but the position effect would be negligible. But as soon as her velocity was relativistic, she would be moving quickly towards Ted, and Ted's apparent size would start to increase, because the velocity effect would be changing very slowly (once the velocity is relativistic the velocity beaming effect doesn't change much) while the position effect would be increasing very rapidly.

 

[PeterDonis]

When Alice is at Bob's position, she sees what Bob sees and both should calculate the same distance based on the same trigonometry

If Alice and Bob are both at rest relative to Ted (i.e., before Alice starts accelerating), then yes, they will both see Ted as having the same apparent size. Their calculation of his distance from that apparent size will only be valid because they have been at rest relative to Ted for the entire time that the light they are seeing was traveling from Ted.

As soon as Alice starts moving relative to Ted, however, she will no longer be at rest relative to Ted for the entire time the light she sees from Ted was traveling, so any calculation she makes of Ted's distance from his apparent size will no longer be valid.

 

[PeterDonis]

When Alice is at Bob's position, she sees what Bob sees and both should calculate the same distance based on the same trigonometry and come up with a distance of 4 LY. When Alice reaches Ted, she should easily calculate a distance of 0 LY. What is the proper method to determine the results of Alice's calculation at an arbitrary point in between?

You are missing the fundamental point that distance is frame dependent. (The only exception is a distance of zero, meaning the two objects are co-located; that is an invariant, true in all frames, but tells you nothing about distances to anything else.) The 4 LY that Alice and Bob calculate at the start (before Alice starts accelerating) are only valid in the frame in which Alice, Bob, and Ted are all at rest. But you could choose some other frame and make the distance anything you like (except zero since Alice and Ted are not co-located).

The same goes for the period while Alice is moving towards Ted; there is no such thing as "the" distance from Alice to Ted. You have to pick a frame. Then you can calculate the distance in that frame, but it won't be valid for any other frame.

 

[jartsa]

Easy-peasy, but a one-word answer is not an explanation.

I'm willing to accept that my method of determining the distance Alice would calculate for Ted is wrong. I still believe she could calculate a distance (based on trig) and that this calculated value could be predicted knowing only the basics that I've described.

When Alice is at Bob's position, she sees what Bob sees and both should calculate the same distance based on the same trigonometry and come up with a distance of 4 LY. When Alice reaches Ted, she should easily calculate a distance of 0 LY. What is the proper method to determine the results of Alice's calculation at an arbitrary point in between?

Alice can calculate the distance that two light rays have traveled using the distance of the two points from where the rays left, and the angle between the rays.

Alice will calculate that the distance is large when she moves towards the light source. Then Alice can also easily calculate the time that the light has traveled. It's a long time if the distance is large.

We know that when Alice calculates the distance to the light source that is a extra short length-contracted distance.

According to Alice the light that Alice sees is old light that left a ruler on distant planet a long time ago. The planet is not a distant planet anymore according to Alice. Because it took a long time for the light to travel the long distance according to Alice, and during that time the planet moved at constant velocity towards Alice, according to Alice.

 

[PeterDonis]

Alice can calculate the distance that two light rays have traveled

Alice can also easily calculate the time that the light has traveled.

Both of these quantities are frame-dependent. Not only that, but by the method you describe, the "distance" and "time" calculated might not match those in any frame.

 

[PAllen]

Sorry I haven't read the whole thread, but I just wanted to discuss a bit about direct measurements by an observer on an arbitrary noninertial (potentially, wildly accelerating in different directions by different amounts, over their own time) world line, versus modeling by such an observer (I like the term modeling over computation, because computation must be done with respect to some model). In particular, how this relates to the use of momentarily comoving inertial frames (hereafter MCIF).

1) The arbitrarily moving observer and an MCIF will agree on any direct measurement that is effectively instant, e.g. camera picture, an observation of frequency of a light source (and thus Doppler), the angular size of something, etc.

2) They will not agree on any observation that takes any significant amount of time, e.g. radar ranging for distance determination, or even rate of change of any of the examples in (1).

3) Models of the direct measurements using the MCIF are typically absurd for the non-inertial observer. For example, consider observation of the change in angular size of some known body (size in its rest frame known), along with its color (also assuming it is known what color it is in its rest frame). Under the assumption that ones own motion is inertial and thus can be taken to be at rest, you can readily model the distance (at time of emission) and speed (at time of emission) of the body corresponding to your current observation, and thus also how long ago your current observation was emitted. However, none of these modeling assumptions make any sense for a non-inertial observer. For example, since your past motion is different from the past of the MCIF, a distance at emission valid for the past of of the MCIF cannot be sensible for a non-inertial observer, whose past positions are known to be very different from the MCIF. Thus, a relation of some observed angular size to e.g. 1 light year for the MCIF - of the body at time of emission - cannot possibly be sensible for the accelerated observer who would be in a completely different location a year ago. They would say, if the observed body was 1 ly away from the MCIF observer a year ago, and the MCIF observer was very far from me a year ago, that observed body could not possibly be 1 ly away from where I was a year ago.

 

[jartsa]

Both of these quantities are frame-dependent. Not only that, but by the method you describe, the "distance" and "time" calculated might not match those in any frame.

Well, I thought Alice's trigonometrical calculations would be correct in Alice's instantaneuosly inertial rest frame.

 

[PeterDonis]

I thought Alice's calculations would be correct in Alice's instantaneuosly inertial rest frame.

I suggest reading @PAllen's post #43.

 

[Freixas]

You are missing the fundamental point that distance is frame dependent.

I'm not going to agree that I am missing this fundamental point, but I'll agree that there are related problems.

The trigonometric calculation's problem is that, while the height of the ruler is not affected by velocity (as it is perpendicular to the direction of travel), the distance to the ruler is because it is in the direction of travel. The trigonometry assumes that opposite vs. adjacent are measured in the same frame, which is not going to be the case for most frames.

The simple proof is just to imagine that at time 0 Alice was co-located with Bob, saw exactly the same image of Ted as Bob, but was traveling at a constant 0.8c. Her distance to Ted would be 2.4 LY, not 4 LY, which is what Bob would say.

The calculation from my simulation has the problem that distances are in different frames when the light leaves Ted and when Alice receives it. I believe can use this method to determine what clock time Alice sees (as opposed to calculates) for Ted, but not for distances.

Thinking back to the formulas I have, if Alice can convert her time (tau) to rest time or distance (using the equations at https://math.ucr.edu/home/baez/physics/Relativity/SR/Rocket/rocket.html), then she it seems she could as easily calculate her distance to other points. But that's just the position I had as the calculated position (the dots with faded colors).

In the end, I wind up with just one position and two different times--the time seen and the time calculated along the IMF's line of simultaneity.

Luckily, none of this has any implications for my tool. It just does the math. If set things up incorrectly, it will apply the math incorrectly.

 

[PeterDonis]

The trigonometry assumes that opposite vs. adjacent are measured in the same frame

There is no such thing as "measured in a frame". Measurements are invariants; their results aren't frame-dependent. When physicists talk about something like a "distance measurement" being frame-dependent, they are really talking about different measurements (for example, measurements made using different rulers that are moving relative to one another).

What the calculation of distance from angle that you describe does assume is that Alice and Ted are at rest relative to each other during the entire time the light is traveling. I have already pointed this out. To put it more precisely, if Alice and Ted are at rest relative to each other (and moving inertially--I did not include this part previously, but it's also necessary), then their common state of rest picks out a particular inertial frame, the one in which they are both at rest, and either one can calculate the distance to the other using trigonometry in the way you describe. To be even more precise, the distance so calculated is the invariant length along a spacelike curve that goes from one to the other and is orthogonal to both of their worldlines; that is the frame-independent way of describing it.

But as soon as either one moves relative to the other, or as soon as either one accelerates and becomes non-inertial, the output of the trigonometry calculation no longer has any physical meaning as a distance. The reason is that there is no longer any spacelike curve that satisfies the invariant requirements I stated just now.

The simple proof is just to imagine that at time 0 Alice was co-located with Bob, saw exactly the same image of Ted as Bob, but was traveling at a constant 0.8c.

If she is traveling at 0.8c relative to Bob when they are co-located, she will not see exactly the same image of Ted as Bob, because of the relativistic beaming effect and the relativistic Doppler shift. I have described in post #38 how her observations would differ from Bob's (Bob would be "Observer A" in that post, and Alice would be either "Observer B" or "Observer C" depending on which direction she is moving).

Her distance to Ted would be 2.4 LY, not 4 LY, which is what Bob would say.

This distance is not something she could calculate using trigonometry as you describe. (Note also that it is not a "distance" that satisfies the invariant requirements I stated above: the spacelike curve that has that length is orthogonal to Alice's worldline at the point where Alice is co-located with Bob, but it is not orthogonal to Ted's worldline at the point where it crosses it--which is not the same as the point where the spacelike curve between Bob and Ted that has length 4 LY crosses Ted's worldline. Note that Bob's curve is orthogonal to both Bob's and Ted's worldlines, and so does meet the invariant requirements I gave above.)

I believe can use this method to determine what clock time Alice sees (as opposed to calculates) for Ted

I don't understand what "method" you would use for this. You certainly can't use trigonometry. The way a relativity physicist would normally do this would be to use a single frame, such as the one shown in the diagram in your OP, to assign coordinates to events, and then calculate the appropriate null worldlines for light rays from Ted to Alice. (In simple enough scenarios you can even get pretty good results by just drawing the null worldlines as 45 degree lines on the diagram.) The time on Ted's clock when a given light ray leaves Ted is the time Alice will see on Ted's clock when the same light ray reaches Alice.

Thinking back to the formulas I have, if Alice can convert her time (tau) to rest time or distance

These will be coordinate times and distances in the original rest frame, which in your case is the frame shown in the diagram in your OP. However, to use those formulas to obtain coordinate times from Alice's clock times, you would have to know Alice's clock times. As you have set up the scenario in your OP, you don't; you know coordinate times and distances in the original rest frame (since you know the equations of the worldlines of Alice, Bob, and Ted in that frame), but you have to calculate Alice's clock times. (Bob's and Ted's clock times are simple because they are always at rest in the given frame, so their clock times are the same as coordinate time in that frame.)

 

[PeterDonis]

none of this has any implications for my tool. It just does the math.

There's still the question of what math it is doing, though. So far I am not convinced it's doing the correct math for anything meaningful.

 

[PeterDonis]

it seems she could as easily calculate her distance to other points.

You say you are not missing the fundamental point I made, but this statement indicates that you still are. There is no such thing as "her distance to other points" without specifying a frame. Since you did not specify a frame in the statement quoted above, that statement is meaningless.

And specifying a different frame for each point on Alice's worldline does not count as specifying a frame. You have to pick one frame to cover the entire extent of Alice's worldline that you are interested in (i.e., where she is sending or receiving any light signals of interest or experiencing any other events of interest). If Alice is accelerating and you want her to always be at rest in your chosen frame, you have to pick a single non-inertial frame (the obvious one for constant proper acceleration is Rindler coordinates, as I think @Ibix pointed out in an earlier post--but since Alice only starts accelerating at a particular point, you would have to use Rindler coordinates only after that point).

 

[PeterDonis]

You have to pick one frame to cover the entire extent of Alice's worldline that you are interested in

And that same frame also has to cover the entire extend of any other worldlines that you are interested in, in this case Bob's and Ted's.