How to calculate each car tyre load during cornering?

[Sprotz]

This is about vehicle physics. I know how to calculate weight on each axle on a car during deceleration. Given the picture below:

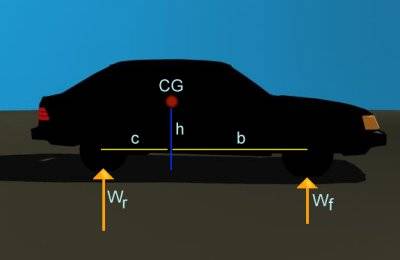
The weight on the front axle is calculated as:
Wf=(c/L)*W-(h/L)*M*a
and the weight on the rear axle is calculated as:
Wr=(b/L)*W+(h/L)*M*a
where c and b are the distances between the center of gravity and the rear and front axle respectively, L is the wheelbase, W is the weight of the car (m*g), h is the height of the center of gravity, M is the mass and a is deceleration.
Now how do I determine the weight on each of the four wheels when the car is cornering? I figured that I could use the area on each corner for each wheel that is inversely proportional to the load. The area calculated by the shifted weight determined by the velocity vector of the car while it is skidding when cornering, as shown in the picture below:

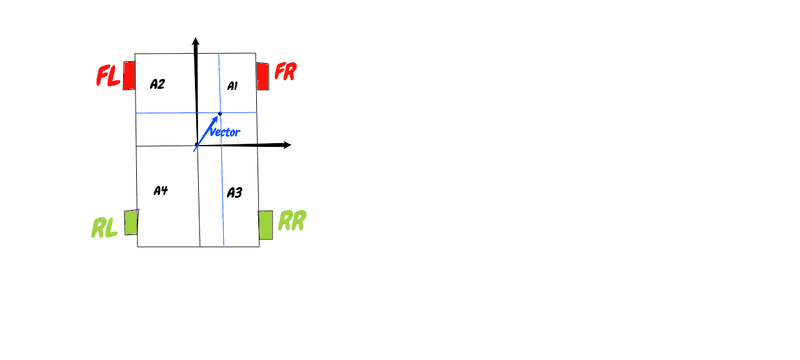
Example, as shown above, the load on the front right wheel (FR) is inversely proportional to the area (A1) as the car's 'reversed' deceleration vector shifts the center of mass to the point shown by blue arrow. Likewise for the other three wheels.
So how do I translate the equations from the first image above into the second image involving each individual wheel?
Or is there another method or simpler method of determining the weight load on each wheel instead of just on each axle?

 

[Nugatory]

So how do I translate the equations from the first image above into the second image involving each individual wheel?
Or is there another method or simpler method of determining the weight load on each wheel instead of just on each axle?

I don't know if it is possible. A moving car is much harder to analyze because so much depends on the details of the suspension design and how it responds to body roll and lateral and transverse accelerations.

For example: The load on a wheel is clearly zero if that wheel lifts off the ground. There are cars that lift their inside front wheel during hard cornering until the suspension is modified (usually by adding a roll bar), so the suspension modifications clearly make a difference - but there's no allowance for these mods in your model. Even straightline acceleration and braking transfers weight between the front and rear wheels in ways that depend on the suspension design (google for "anti-squat anti-dive").

So I'm expecting that you'll need an appreciably more complicated set of equations than what can be derived from the straightforward static analysis of the car when it's not moving. look at what the racers are doing and you'll probably find enough to get yourself started.

 

[Sprotz]

Let us assume that the suspension hardness is constant and equal on all tyres. There has to be a fairly simple equation to find the load on each tyre. It does not have to be overly realistic. I simply need to simulate spin out / oversteer while cornering by reducing traction on the rear wheels.

 

[anorlunda]

How can you calculate spin out without considering roll over?

 

[Sprotz]

I have the physics set up already for that. All I need are the wheel loads.

 

[A.T.]

I figured that I could use the area on each corner for each wheel that is inversely proportional to the load.

How did you derive this? Where does the height of the center of gravity appear in your method?

 

[Sprotz]

How did you derive this? Where does the height of the center of gravity appear in your method?

I simply added another dimension. The first method has a linear dimension, forward and back, and the weight distribution is calculated by length, so I thought that adding a second dimension (sideways), made sense to calculate weight distribution as area (length*width). The second picture is a top-down view so height of the center of gravity could not be shown easily.

 

[Nugatory]

Let us assume that the suspension hardness is constant and equal on all tyres. There has to be a fairly simple equation...

Depends on what you consider to be fairly simple, but yes...

to find the load on each tyre. It does not have to be overly realistic. I simply need to simulate spin out / oversteer while cornering by reducing traction on the rear wheels.

If you're just looking for a moderately realistic simulation (say for a video game where all that matters is that you get plausible car-like behavior, as opposed to a result that is quantitatively correct for a specific car) you can choose a reasonable value for the location of the roll center and the center of gravity of the car. A google search for "chassis suspension dynamics" will find the equations you're looking for from there.

 

[FactChecker]

It sounds like you only want a believable simulation rather than an analysis tool. For analysis, there are so many factors to consider like road conitions, tire conditions, tread design, wind, road banking, etc., that you will probably not want to use physics equations to any significant extent. You may want to just include some parameters that control slip as a function of g's and adjust the parameters till the simulation looks reasonable.

 

[Sprotz]

Ok, thanks. I've found a pdf ebook that discusses vehicle simulation in games, and includes weight transfer during cornering.
link: https://nccastaff.bournemouth.ac.uk/jmacey/MastersProjects/MSc12/Srisuchat/Thesis.pdf

 

[jim mcnamara]

@Ranger Mike has a lot of practical experience, and there may be some free/opensource software that would help. Tire loading during cornering is really important in automobile racing.