How fast will two spinning weighted wheels propel a 7 lb cylinder?

[spike3333]

Hello,

I am hoping someone on the forum can help me. I am designing a machine to move a cylindrical weight between to high speed rollers.

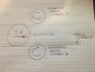
The system is comprised of two weighted drive wheels being spun by motors positioned one above the other as shown in the sketch. The weighted drive wheels are 6 lb each and are 4.25" in diameter and 1.6" wide. A 7 lb cylinder 8.5" in dia and 10 in wide is rolling toward the spinning drive wheels on a guiding track at 2 miles and hour. The drive wheels are spaced so they both make contact with the passing cylinder. The surface of the drive wheels is a slightly compressible elastomer. The passing cylinder has a urethane surface. My question is how fast will the cylinder be propelled assuming that both motors are:

DC 24V 150W 775 Electric Motor 3500 RPM no load spinning at max RPM

Alternately

DC 24 V 150W ZY6812 Electric Motor 13000 RPM no load spinning at max RPM

I can vary the speed of both the motors relative to each other as well. I can also vary the amount of compression of the surface of the wheels by varying the space between the centers of the wheels. I assume there is an optimal spacing but don't know how to determine it.

Also, are these motors my best candidates? What properties of the motors should I be prioritizing. Is there an equation that could be developed that I could predict the speed of the cylinder. Will altering the surface texture of the wheels hurt or help me?

Thanks,

Dwight

 

[jrmichler]

Is there an equation that could be developed that I could predict the speed of the cylinder.

There is an optimal spacing, and a thought experiment will show how to find it. If the spacing is too large, the drive wheels will skid on the cylinder, and the cylinder will not reach the speed of the drive wheels before it exits the drive wheels. If the spacing is slightly too small, energy will be lost over compressing the drive wheels. If the spacing is much too small, the cylinder will jam between the drive wheels.

Then, you need to consider the speeds of the two drive wheels. If they run the same speed, the cylinder is not rotating when it leaves the drive wheels. It would then skid on the track surface until it starts rotating fast enough to roll without skidding. Or you can run the drive wheels at different speeds so that the cylinder rolls without skidding when it leaves the drive wheels. What should the relative speeds of the two wheels be?

Hint: What is the speed of the wheel surface at the point in contact with the track relative to the track surface when it is rolling without skidding.

Think about this for a while, then come back, and we will help you take it further.

 

[spike3333]

To assist in the calculation, the cylinder is dropped into the machine through a chute with Delrin rails via gravity until it engages the drive wheels. After it engages the drive wheels it continues on Delrin rails until it exits the machine. The goal is to propel the cylinder at the maximum speed possible with two 150 W DC motors of comparable size to the samples stated. I would assume that you would want the lower motor to match the speed of the cylinder as it engages the drive wheel and the upper motor to be at maximum speed.

I included a profile of the path through the machine to calculate the cylinder's velocity due to gravity at the point it contacts the drive wheels

 

[256bits]

I would assume that you would want the lower motor to match the speed of the cylinder as it engages the drive wheel and the upper motor to be at maximum speed.

Makes sense.
You should re-read the Hint from jrmichler once more.
Do you want to shoot the cylinders out, or roll them out?
Do you really need the bottom drive roller? if rolling them out.

 

[spike3333]

I definitely want the cylinder to roll at max speed. OK, so having a drive wheel on the bottom defeats that and it can be eliminated. That makes the device much simpler.

How do I determine the best spacing (between drive wheel surface and opposing rails) and drive wheel surface configuration? The surface of the cylinder is a smooth urethane. My goal is to have the cylinder reach 20 mph. Is that doable?

Since I don't neccessarily care how long the drive wheel takes to get up to speed (30 sec is fine), should I maximize motor RPM or is torque equally important?

 

[Gunnir]

To simplify everything above; it looks like the cylinder is rolling prior to hitting the motors. So whatever energy you give the cylinder through the motor will be both linear momentum and angular momentum - and it looks like you care about hitting 20 mph linearly?

If so - is it possible to just place the motors to contact the flat end of the cylinders? Rotate those motors then at 20 mph. It will inevitably skid however, and once it starts rolling again; it will translate the linear momentum given by the motors to rotational; slowing the cylinder. But simplifies your problem significantly lol

Also is it rolling along it's central axis via these Delrin rails? Or is it rolling along it's curved outer radius? If the former, the above solution would work with higher accuracy

 

[jrmichler]

Since the contact time is short, and motor torque will be low, the primary driver will the drive wheel inertia. Calculate wheel speed by assuming that the cylinder is leaving at the desired speed, and that the surface speed of the drive wheel is equal to the surface speed of the cylinder at that time. Then use conservation of momentum to calculate the speed of the drive wheel just before it contacts the cylinder.

Note that the initial contact between the drive wheel and cylinder will be skidding, then that will change when the cylinder gets up to speed. Kinetic energy is not conserved in this system.

You can design the inlet guide rails to increase the duration of contact between the drive wheel and cylinder. This would allow you to use less contact pressure and reduce overall forces.

 

[spike3333]

Yes, the cylinder is dropped into the shoot from above and is rolling when it engages the wheels. Yes, I want to reach 20 MPH or as close to it as I can.

I don't see how driving the cylinder from the end is more efficient or simpler, especially if a motor can be eliminated. Can you explain why you feel it would be?

Yes, the cylinder is rolling down Delrin rails in such a way that the cylinder is kept centered while it is rolling.

 

[spike3333]

So if I want the cylinder to roll at 20 MPH and it is 8.5" in diameter it's circumference is 26.70" and will roll 26.70" in one revolution. So the ball will need to roll at 791 RPM. The wheel has a circumference of 13.35" so it will need to spin at 1582 RPM.

How do I determine the reduction in motor RPM for either of them spinning a 6 lb weight?

Also, now that I am only using a single motor, there is only one wheel supplying the momentum. How do I determine if one weighted wheel is sufficient?

 

[jrmichler]

Now you know the velocity of the cylinder and the drive wheel at the time that the cylinder leaves the drive wheel. Keeping in mind that the cylinder has both angular and translational velocity, and thus momentum, calculate the momentum of the cylinder. Also calculate the momentum of the drive wheel. You need the mass of the cylinder, and the rotational inertia of both the cylinder and the drive wheel.

You are assuming a small motor, so it follows that the work of accelerating the cylinder will be done by decelerating the drive wheel. The effect of motor torque will be small compared to the effect of drive wheel inertia. The loss in momentum of the drive wheel will be equal to the gain in momentum of the cylinder. Adding the leaving momentum of the cylinder to the leaving momentum of the drive wheel will give you the necessary momentum of the drive wheel just before the cylinder makes contact. Once you know the momentum, you can calculate the RPM. That will be the RPM that you need to spin the drive wheel.

If the necessary RPM is ridiculously fast, then redesign the drive wheel for more inertia.

Hint: Expect this to be an iterative process.

 

[hutchphd]

So if I want the cylinder to roll at 20 MPH and it is 8.5" in diameter it's circumference is 26.70" and will roll 26.70" in one revolution. So the ball will need to roll at 791 RPM. The wheel has a circumference of 13.35" so it will need to spin at 1582 RPM.

Don't forget that the top of an automobile tire is moving forward at twice the speed of the car...

 

[spike3333]

Now you know the velocity of the cylinder and the drive wheel at the time that the cylinder leaves the drive wheel. Keeping in mind that the cylinder has both angular and translational velocity, and thus momentum, calculate the momentum of the cylinder. Also calculate the momentum of the drive wheel. You need the mass of the cylinder, and the rotational inertia of both the cylinder and the drive wheel.

You are assuming a small motor, so it follows that the work of accelerating the cylinder will be done by decelerating the drive wheel. The effect of motor torque will be small compared to the effect of drive wheel inertia. The loss in momentum of the drive wheel will be equal to the gain in momentum of the cylinder. Adding the leaving momentum of the cylinder to the leaving momentum of the drive wheel will give you the necessary momentum of the drive wheel just before the cylinder makes contact. Once you know the momentum, you can calculate the RPM. That will be the RPM that you need to spin the drive wheel.

If the necessary RPM is ridiculously fast, then redesign the drive wheel for more inertia.

Hint: Expect this to be an iterative process.

Before iterating a redesign of the drive wheels, I would like to determine the maximum speed I can achieve with the motors I have initially selected.

Am I looking at conservation of kinetic energy? The cylinder has x kinetic energy as it drops the 11.27" to the wheel. The wheel has y kinetic energy prior to the cylinder making contact. Is the loss of kinetic energy of the wheel gained by the cylinder allowing it to achieve a speed of z. If so, how do I determine how fast the motor can spin the 5 lb mass of the wheel if I assume it is allowed to reach max RPM? I know what the no load RPM of the motors are but how is that speed effected by weight. Is that calculated using the power curves of the motors?

 

[jrmichler]

1) Go back and reread Post #7, especially the second paragraph.

2) The motor performance curve (torque vs RPM) allows you to calculate the time to accelerate the drive wheel up to speed. That speed will be the speed at which the motor torque is equal the the friction torque in the system. It should be close to the no load speed. Weight, or more correctly, inertia only affects the time to accelerate. The wheel inertia has English units of inch-lb-sec^2.

 

[spike3333]

1) Go back and reread Post #7, especially the second paragraph.

2) The motor performance curve (torque vs RPM) allows you to calculate the time to accelerate the drive wheel up to speed. That speed will be the speed at which the motor torque is equal the the friction torque in the system. It should be close to the no load speed. Weight, or more correctly, inertia only affects the time to accelerate. The wheel inertia has English units of inch-lb-sec^2.

OK, I see that Kinetic Energy is not conserved and momentum is. I know the momentum of the ball is it's mass times it's velocity but I don't understand how to calculate the momentum due to rotation of the cylinder or the wheel.

Isn't there a limit to the mass the motor can spin? How do I know if I'm approaching it? Would the RPM achieved (assuming time is not considered) be a horizontal line relative to weight until it suddenly drops to zero?

 

[jrmichler]

To calculate momentum, use search term angular momentum.

Inertia is inertia, torque is torque, RPM is RPM, and acceleration equals torque divided by inertia. If the motor is producing torque at a certain RPM, then it is accelerating the drive wheel. When the RPM reaches the point on the motor performance curve where the torque goes to zero, that's when it stops accelerating and stays at a constant speed. The equation is $T = I \alpha$, where T is torque, I is inertia, and $\alpha$ is acceleration, with all variables in consistent units.

This ignores bearing friction. Bearing friction can usually be ignored if the drive wheel is mounted directly on the motor shaft. A small drive motor connected to a large drive wheel may require outboard bearings. In that case, the bearing friction must be added into the calculations. Just subtract bearing friction from the motor torque to get a torque curve of available torque to accelerate the drive wheel.

So, yes, there is a limit to the mass the motor can spin. When the bearing friction from the bearings needed to support the mass is greater than the motor torque, the motor will not be able to spin the mass.

 

[spike3333]

The cylinder reaches 4.3 MPH just before contacting the wheel, so initial translational momentum (mv) of the cylinder is 30.1 (lb⋅M)/H. For an object rolling without slipping, the angular velocity is equal to the translational velocity divided by the radius so the angular momentum (mvr) of the cylinder just prior to contacting the wheel is 3.25 lb⋅(M²/H). The translational momentum of the wheel just prior to contact is 0 and the rotational momentum is about 61000 lb⋅(M²/H) assuming the motor can reach 10,000 RPM. The magnitude of the number seems illogically high but I don't have anything from experience to compare it to. I also don't understand how the decrease in the translational momentum of the wheel contributes to the increase in translational momentum of the cylinder after contact.

 

[jrmichler]

Next steps:
1) Decide on a consistent set of units.
2) What is the mass and rotational inertia of your cylinder in your consistent set of units?
3) You have given a desired speed for the cylinder. What is that speed in your consistent set of units? What is the total (translational plus rotational) momentum of the cylinder at that speed? Have you figured out how to deal with translational plus rotational momentum?
4) If the drive wheel surface speed matches the cylinder speed at discharge, what is the momentum of the drive wheel at that speed? Consistent units!
5) Since total momentum is conserved, what must be the momentum of the drive wheel before contacting the cylinder?
6) Calculate the necessary drive wheel RPM.

 

[spike3333]

1) units; miles - mi (incorrectly used M), lbs and hour - hr (incorrectly used H)
2) mass of cylinder is 7 lbs. Rotational inertia is I = mr² = 0.019 lb⋅mi²
3) desired speed is 20 mi/hr, I have not figured out how to deal with translational plus rotational momentum. What is confusing to me is that the resultant rotational momentum has a distance squared and the translational doesn't.
4) I know I want the surface of the wheel to be traveling at 20 mi/hr. I don't know how to determine the momentum of a mass spinning on an axis fixed in space.

Probably understanding how deal with combining the momentums will allow me to calculate the remaining requirements.

 

[jrmichler]

Use standard units. Standard English units would be inches, pounds, and seconds. Your inertia is wrong by about nine orders of magnitude.

Your description of the desired speed is unclear. Is the center of the cylinder moving with a linear velocity of 20 MPH? If so, say so. Then find the rotational speed of the cylinder standard units (radians per second).

 

[jrmichler]

Geez, I hope I didn't scare @spike3333 off. The necessary speed can only be calculated after the known information is fully understood.

The key problem here is how to calculate a case where there is both translational and angular momentum, as shown in the sketch below. The round cylinder is rolling without slipping on a flat surface. It makes contact at point O. It is acted on by a force F that is tangential to the top of the cylinder and parallel to the surface.

Point O is an instantaneous center, and the cylinder rotates about that point. Since the cylinder rotates about that point, it has rotational inertia about that point. That inertia is the rotational inertia about the center of mass, plus additional (parallel axis theorem) inertia due to the axis of rotation being displaced from the centroidal axis of the cylinder. The rotational inertia of a solid cylinder is 0.5*M*R^2, and the additional inertia at point O is M*R^2. Note that a typical drive wheel is not a simple cylinder, so calculating the inertia of a drive wheel is a little more complex.

For an cylinder subject to only one force (no friction), the change in momentum is equal to the force impulse. The force impulse is the force (magnitude and direction) times the duration. The total change in momentum is equal to the impulse, regardless of the duration of the impulse. A high force for a short time, and a low force for a longer time, will drive the same change in momentum if the two force impulses are the same. That allows us to make the time arbitrarily short, and just calculate the impulse.

The linear velocity of the cylinder is known as it enters the drive wheel, it is also known as it leaves the drive wheel. Assume that it is in contact with the drive wheel for arbitrarily short distance, then there is a sudden increase in speed, and thus momentum. That increase in momentum is equal to the force impulse from the drive wheel.

The drive wheel is subject to an equal and opposite force impulse. The same force impulse that caused the cylinder to speed up, also caused the drive wheel to slow down. The speed and momentum of the drive wheel immediately after driving the cylinder is known (equal surface speeds). The momentum of the drive wheel immediately before contacting the cylinder is equal to the drive wheel momentum after the cylinder leaves contact plus the change in momentum from the force impulse.

Last step: Knowing the momentum of the drive wheel immediately before contacting the cylinder, calculate the RPM. That's the RPM the to which the motor has to accelerate the drive wheel in order to drive the cylinder to the desired speed.