sherrellbc
- 83
- 0
I am consistently getting this wrong. To me, in the picture below, it would make sense that the structure would be pulling downward, and the cable BD would be pulling upward - thus the system is in equilibrium.
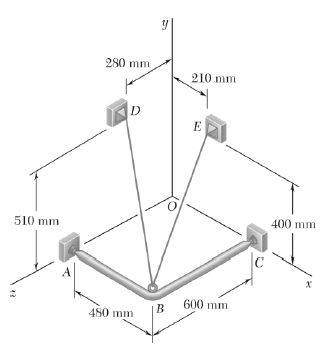
However, the solution to this problem show the force being applied downward onto the structure:
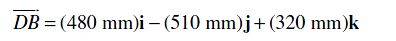
What is the trick?
However, the solution to this problem show the force being applied downward onto the structure:
What is the trick?