morrw1ndy
- 4
- 0
1. Homework Statement
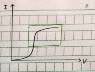
How to determine the change of R of a non-ohmic conductor from different parts of I-V graph?
Please see the sketch attached.
Homework Equations
R=V/I
The Attempt at a Solution
For the part that passes through the origin, it is obvious that the reciprocal of the gradient, i.e. dV/dI, shows how R changes.
However, for the upper part(green part), since it does not passes though (0,0), the gradient only shows how I changes with V, but not how R changes with V.
I have tried to sub in numerical values as shown in the second picture, it seems that R varies in different ways even though I-V graph is concaving downwards.
Instead of sketching a separate R-V graph, are there any alternatives to tell the change in R directly from the graph?
Thanks a lot.