How to determine the power of this circuit?

[Leonid92]

Homework Statement

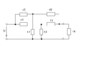
Determine power of the circuit (Fig. 1), if voltage U = 20 V, resistances of branches: r1 = r4 = 5 Ohm, r2 = r3 = 2 Ohm, r5 = r6 = r7 = 6 Ohm.

Relevant Equations

U(input) = A*U(output) + B*I(output)
I(input) = C*U(output) + D*I(output)
A*D - B*C = 1

In "Homework Equations" field, I wrote general equations for quadripole.
I have doubt about the solution. True answer given in the electrical engineering textbook is P = 100 W.
Here is my solution:
1)
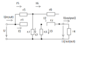
In scheme, I pointed currents and U(output) (Fig. 2).

2)
U = A*U(output) + B*I2
I1 = C*U(output) + D*I2
A = 1 + r1/r3
B = r1 + r2 + (r1*r2)/r3
C = 1/r3
D = 1 + r2/r3

3)
U = A'*U(output) + B'*I6
I5 = C'*U(output) + D'*I6
A' = 1 + r5/r7
B' = r5 + r6 + (r5*r6)/r7
C' = 1/r7
D' = 1 + r6/r7

4)
U(output) = I(output)*r4

5)
U = A*I(output)*r4 + B*I2
I1 = C*I(output)*r4 + D*I2
U = A'*I(output)*r4 + B'*I6
I5 = C'*I(output)*r4 + D'*I6
I(output) = I2 + I6

6)
U = A*(I2 + I6)*r4 + B*I2
I1 = C*(I2 + I6)*r4 + D*I2,
U = A'*(I2 + I6)*r4 + B'*I6
I5 = C'*(I2 + I6)*r4 + D'*I6

7)
A = 3.5
B = 12 Ohm
C = 0.5 S
D = 2
A' = 2
B' = 18 Ohm
C' = (1/6) S
D' = 2

8) Substitute numbers into the system of equations:
20 = 29.5*I2 + 17.5*I6, (1)
I1 = 4.5*I2 + 2.5*I6, (2)
20 = 10*I2 + 28*I6, (3)
I5 = (5/6)*I2 + (17/6)*I6, (4)

(1) - (3):
19.5*I2 - 10.5*I6 = 0
I2 = (21*I6)/39

(3):
20 = 10*(21*I6)/39 + 28*I6
I6 = (130/217) A

I2 = (21*I6)/39 = (10/31) A

(2):
I1 = 4.5*(10/31) + 2.5*(130/217) = 2.95 A

(4):
I5 = (5/6)*(10/31) + (17/6)*(130/217) = 1.97 A

9)
I(input) = I1 + I5 = 4.92 A

10)
Power of the circuit:
P = I(input)*U = 98.4 W.

Is it right solution?

In the textbook, many answers are rounded, so the answer I obtained does not contradict the answer specified in the textbook.

 

[ehild]

Homework Statement: Determine power of the circuit (Fig. 1), if voltage U = 20 V, resistances of branches: r1 = r4 = 5 Ohm, r2 = r3 = 2 Ohm, r5 = r6 = r7 = 6 Ohm.9)
I(input) = I1 + I5 = 4.92 A

10)
Power of the circuit:
P = I(input)*U = 98.4 W.

Is it right solution?

In the textbook, many answers are rounded, so the answer I obtained does not contradict the answer specified in the textbook.

I solved the problem with nodal analysis, and I got I(input)=4.91 A. Your solution looks correct.

 

[AVBs2Systems]

Hi

I thought I might add this quick and easy online circuit simulator, that would help you when practicing questions:

https://www.falstad.com/circuit/