How to ensure maximum possible joint torque for an actuator?

[TheShermanTanker]

Below, I have a joint system that consists of a fixed anchor and a moving arm:

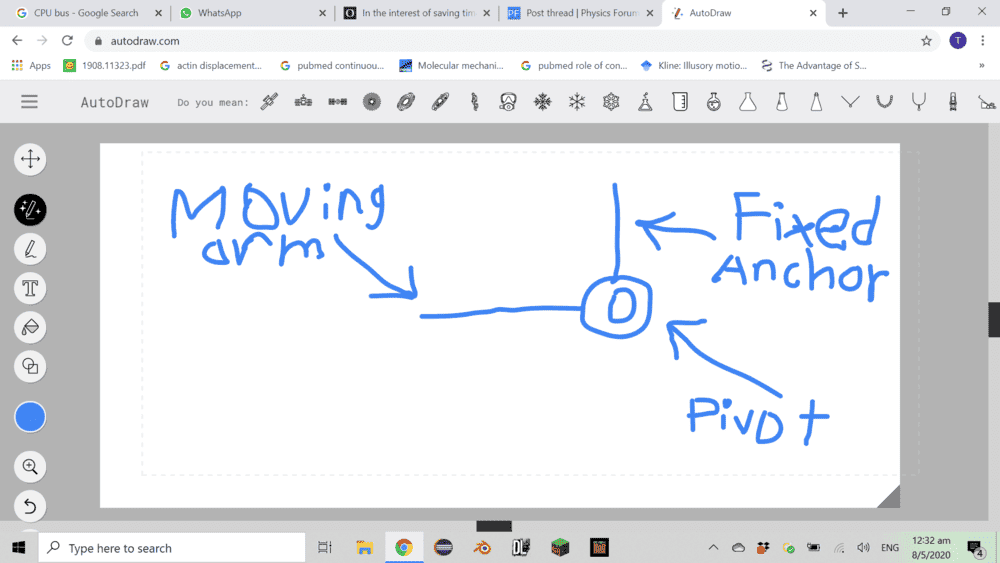
What I want is simple: To attach a linear actuator on the moving arm in such a way that the mechanical advantage of the actuator is exactly 1 (Ie the actuator only has to generate exactly the amount of force as the load on the moving arm)

This may seem simple at first glance, just attach the actuator at the far end of the moving arm, right?

But there is a necessary constraint: The other end of the actuator has to be fixed to the fixed arm AND has to be as close to the moving arm as possible, I can't just stick the other end to anywhere I want. So now I end up with this:

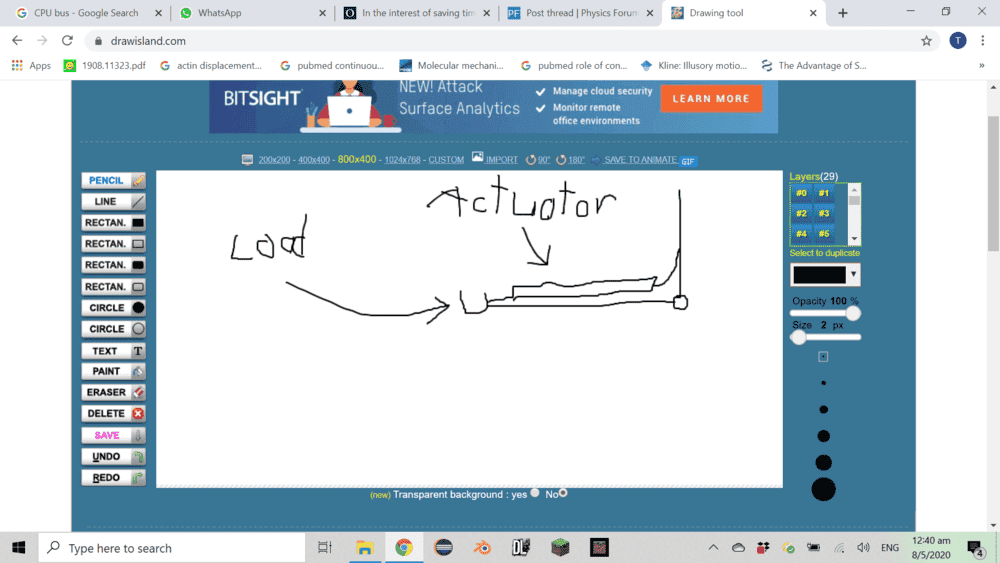
The problem is that torque generated depends on perpendicular distance to the pivot. So no matter how far out I fix the actuator, it's still at a mechanical disadvantage, since the actual perpendicular distance to the pivot is very small

Anyone know how I can fix this issue?

 

[berkeman]

Why not just fix the actuator to the moving arm? It just needs to push the load straight away from the end of the moving arm, right? Why does this force need to be transferred to the fixed arm through anything but the pivot bearing?

I guess I'm not understanding your problem statement so far...

 

[A.T.]

But there is a necessary constraint: The other end of the actuator has to be fixed to the fixed arm AND has to be as close to the moving arm as possible,

That's not a constraint, but an optimization goal.

I can't just stick the other end to anywhere I want.

That's an ill-defined constraint.

(Ie the actuator only has to generate exactly the amount of force as the load on the moving arm)

That's a constraint.