Dale12
- 17
- 1
In Feynman's lectures, he explained the ##TE_{10}## mode of waveguide by considering a line source in the middle of waveguide as below:
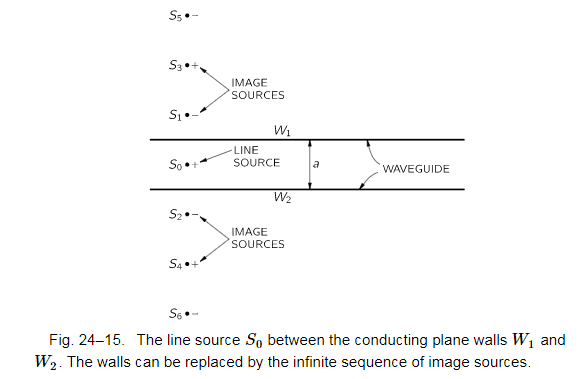
since the adjacent sources are all out-of-phase, which means to have interference, the adjacent optical path would be about half of wavelength as below:
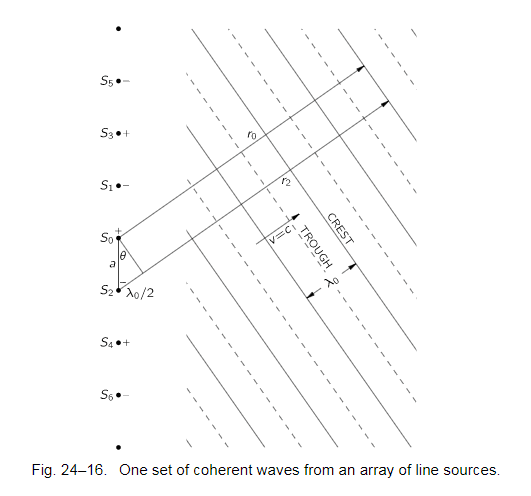
where
$$\sin\theta = \frac{\lambda_0}{2a}$$ (24.33)
and the relationship between wavelength in waveguide and free-space is show in this picture:
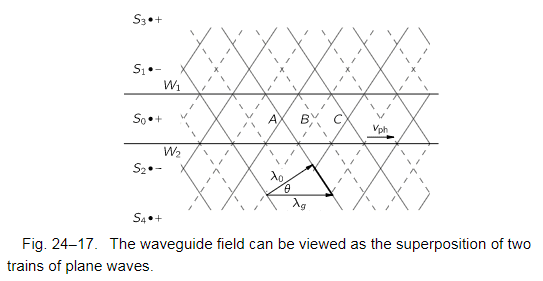
and we have:
$$\cos\theta = \frac{\lambda_0}{\lambda_g}$$,
combing with ##\sin\theta = \frac{\lambda_0}{2a}##, we have:
$$\lambda_g = \frac{\lambda_0}{\cos\theta} = \frac{\lambda_0}{\sqrt{1-(\lambda_0/2a)^2}}$$
Feynman then summarized with:
“ If the frequency is high enough, there can be two or more possible directions in which the waves will appear. For our case, this will happen if ##\lambda_0<\frac{2}{3}a##. In general, however, it could also happen when ##\lambda+0<a##. These additional waves correspond to the higher guide modes we have mentioned. ”
However, ##\lambda_0<\frac{2}{3}a## is corresponding to ##TE_{30}## modes and the differential phase between adjacent source is about 3/2 wavelength, but how to explain ##\lambda+0<a## which corresponding to one wavelength or ##TE_{20}## mode?
Thanks!
since the adjacent sources are all out-of-phase, which means to have interference, the adjacent optical path would be about half of wavelength as below:
where
$$\sin\theta = \frac{\lambda_0}{2a}$$ (24.33)
and the relationship between wavelength in waveguide and free-space is show in this picture:
and we have:
$$\cos\theta = \frac{\lambda_0}{\lambda_g}$$,
combing with ##\sin\theta = \frac{\lambda_0}{2a}##, we have:
$$\lambda_g = \frac{\lambda_0}{\cos\theta} = \frac{\lambda_0}{\sqrt{1-(\lambda_0/2a)^2}}$$
Feynman then summarized with:
“ If the frequency is high enough, there can be two or more possible directions in which the waves will appear. For our case, this will happen if ##\lambda_0<\frac{2}{3}a##. In general, however, it could also happen when ##\lambda+0<a##. These additional waves correspond to the higher guide modes we have mentioned. ”
However, ##\lambda_0<\frac{2}{3}a## is corresponding to ##TE_{30}## modes and the differential phase between adjacent source is about 3/2 wavelength, but how to explain ##\lambda+0<a## which corresponding to one wavelength or ##TE_{20}## mode?
Thanks!