How to Find h(t) in Time Domain for y(t)=x(t)*h(t)?

[asmani]

Suppose that $y(t)=x(t)\ast h(t)$.

($\ast$ denotes convolution)

Here are the signals:

How to find h(t) in time domain? Does there exist such h(t)?

Thanks in advance.

 

[asmani]

Bump!

 

[the_emi_guy]

Using the doublet function:

h(t) =
\begin{cases}
\delta', & \text{for } -\infty < t <0 \\
-\delta', & \text{for } 0 < t < \infty\\
\end{cases}

 

[asmani]

Thanks.

Let's consider the delta function as the limiting case of the following function:

Now, isn't your function the same as $-\delta'(t)$?

 

[the_emi_guy]

The doublet is the derivative of the Dirac delta function.

 

[rude man]

Think Fourier integral!

 

[vela]

You need to show your attempt at solving the problem on your own before you receive help here.

 

[asmani]

A clarification: This thread is moved from electrical engineering forum. Maybe it is a homework or coursework-type question, but actually it's not a homework or a coursework question, and I believe cannot be.

Anyway, here is my attempt:
$$\mathcal{F}\left \{ x(t) \right \}=sinc^2(f)\; ;\: \mathcal{F}\left \{ y(t) \right \}=2sinc(2f)$$
$$\mathcal{F}\left \{ h(t) \right \}=\frac{\mathcal{F}\left \{ y(t) \right \}}{\mathcal{F}\left \{ x(t) \right \}}=\frac{2sinc(2f)}{sinc^2(f)}=4\pi f\cot(2\pi f)$$
I guess that this function has no inverse Fourier transform, and thus there is no LTI system with x(t) as input and y(t) as output. Is this correct? If yes, how to prove?

The doublet is the derivative of the Dirac delta function.

I know that, but for t<0 we have δ_Δ(t)=0, which implies that for t<0, δ_Δ'(t)=0. That's why I think your function is the same as -δ'(t).

 

[the_emi_guy]

Think of it this way...

1 - What kind of circuit would convert your x(t) to your y(t)?

2 - Next, what would be the impulse response of that circuit? This would be your h(t).

 

[rude man]

A clarification: This thread is moved from electrical engineering forum. Maybe it is a homework or coursework-type question, but actually it's not a homework or a coursework question, and I believe cannot be.

Anyway, here is my attempt:
$$\mathcal{F}\left \{ x(t) \right \}=sinc^2(f)\; ;\: \mathcal{F}\left \{ y(t) \right \}=2sinc(2f)$$
$$\mathcal{F}\left \{ h(t) \right \}=\frac{\mathcal{F}\left \{ y(t) \right \}}{\mathcal{F}\left \{ x(t) \right \}}=\frac{2sinc(2f)}{sinc^2(f)}=4\pi f\cot(2\pi f)$$
I guess that this function has no inverse Fourier transform, and thus there is no LTI system with x(t) as input and y(t) as output. Is this correct? If yes, how to prove?

What reason do you have for assuming your H(f) has no inverse? Have you tried doing the integration?

Ref: G.A. Campbell and R. M. Foster, "Fourier Integrals for Practical Applications", D. Van Nostrand 1958.

PS - I did not check to see that you did X(f) and Y(f) correctly ...

 

[asmani]

What reason do you have for assuming your H(f) has no inverse? Have you tried doing the integration?

Ref: G.A. Campbell and R. M. Foster, "Fourier Integrals for Practical Applications", D. Van Nostrand 1958.

PS - I did not check to see that you did X(f) and Y(f) correctly ...

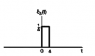
When the plot is as follows, I don't know how to do the integration, if the integral exists.

Think of it this way...

1 - What kind of circuit would convert your x(t) to your y(t)?

2 - Next, what would be the impulse response of that circuit? This would be your h(t).

I guess there is no such circuit/LTI system/h(t). Let's consider two cases:

1. The input to the system S is y(2t), and the output is x(t). We can easily find that the impulse response of S is h(t)=y(2t).

2. The input to the system S' is y(t), and the output is x(t). We can observe that S' is the same S series with another system S'' which gives the output z(2t) for the input z(t). Obviously S'' is not a LTI system, so S' isn't.

That's why I think it's possible that the original system cannot be LTI either.

Thanks.

 

[rude man]

You're not integrating the function you sketched, which I presume is your H(f).
You're trying to integrate ∫H(f)e^jωtdf over f = -∞ to f = +∞ with ω = 2πf.

 

[asmani]

The input to the system S' is y(t), and the output is x(t). We can observe that S' is the same S series with another system S'' which gives the output z(2t) for the input z(t). Obviously S'' is not a LTI system, so S' isn't.

Actually this argument was not correct!

You're not integrating the function you sketched, which I presume is your H(f).
You're trying to integrate ∫H(f)e^jωtdf over f = -∞ to f = +∞ with ω = 2πf.

Of course, that's h(0). Can you help me on this integration?

Thanks.

 

[rude man]

I'm wondering about your initial approach, now that I've looked at it some more.

Looking at your x(t) and y(t) graphs, and taking the Fourier integrals of both,

X(w) = (1/2π)∫(t+1)exp(-jwt)dt from t= -1 to 0 + (1/2π)∫(1-t)exp(-jwt)dt from t= 0 to +1.

Similarly,
Y(w) = (1/2π)∫exp(-jwt)dt from t = -1 to +1.

Then H(w) = Y(w)/X(w) and finally

h(t) = ∫H(w)exp(jwt)dw.

I tried to do the X(w) integration and found it pretty messy, which means subject to making mistakes. I used ∫e^axdx = e^ax/a and ∫xe^axdx = (e^ax/a²)(ax-1).

The Y(w) integration is of course much simpler. The h(t) inverse integral promises to be messy also.

So, best I can do for you is to suggest either you try to muddle through the integrations, or get a table of Fourier integrals like the one I recommended previously. I wish I had that table but I don't.

Of course, it may be that the best approach is graphic convolution, but I'm not inclined to try that myself.

 

[asmani]

I thought these are known results:
http://en.wikipedia.org/wiki/Rectangular_function#Fourier_transform_of_the_rectangular_function
http://en.wikipedia.org/wiki/Triangular_function

 

[rude man]

I thought these are known results:
http://en.wikipedia.org/wiki/Rectangular_function#Fourier_transform_of_the_rectangular_function
http://en.wikipedia.org/wiki/Triangular_function

Thank you! We can now both work this. I'll keep you apprised of any progress.