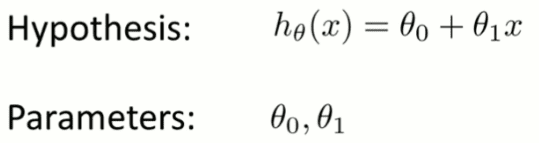Ray Vickson
So let's start little by little... let's talk about the first paragraph.
Lets think we have a dataset ##(X_1,Y_1), \ldots, (X_n, Y_n)##. As you said, it is possible that those points in the xy space form groups. So our task is to find a straight line that is like the 'mean' of those points.
I am going to try to explain it better.
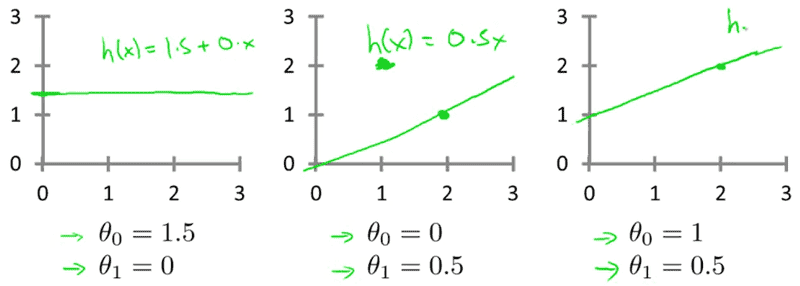
Imagine that we have that cloud of points, so we have to calculate the ##y= a + bx## (the straight line). What happens while calculating the straight line? The problem here is that we have to calculate ##a## and ##b## values to get a straight line that contains the lower amount of errors.
But, what is an error?
We know that is impossible to get a straight line that represents with 100% accuracy all the ##x,y## points in the graph.
A "perfect" case would be this one:
It's perfect (without errors), because all the points belong to the straight line. So any prediction that we would do, givin an ##x_n## value, will output an exact ##Y## value, without errors.
The problem starts when we have some "errors", like this one:
The green (I have used green to make it easier to differentiate) points are not fitted to the straight line. Using linear algebra it's impossible to create a straight line that contains all the points of the graph. So, when we try to predict ##Y## values, the output won't be 100% accurate because it will contain some error percentage.
An error will be the next:
Because the predicted value doesn't represent the real value. There is an error between the ##real value## and the ##predicted value##.
If we analyze a huge amount of points, there will be a huge amount of errors, right?
So our task is to calculate the straight line that contains the lower amount of errors, right? For that reason, it's called "minimization", because we are trying to minimize the total amount of errors, right?