Nur Ziadah
- 34
- 3
I have a few of integration equations and need to convert it into Python. The problem is when I tried to plot a graph according to the equation, some of the plot is not same with the original one.
The first equation is the error probability of authentication in normal operation:
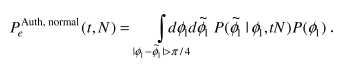
cond equation is the error probability of authentication under MIM attack:
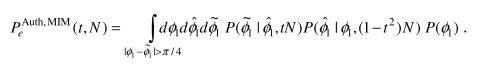
The error probability of authentication in normal operation can be calculated by:
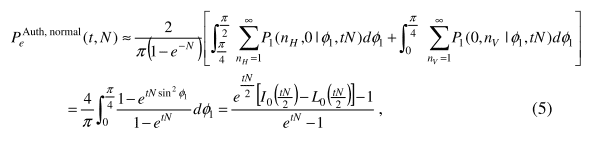
Supposedly, the graph (original) will be shown like this:

y-axis: error probability
x-axis: N
Pe^normal = blue lines
Pe^MIM = red lines
Differences between two error probabilities (Pe^MIM - Pe^normal)= green lines
I tried to code it into Python and this is my full codes:
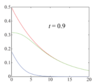
The graph produce from my code is:
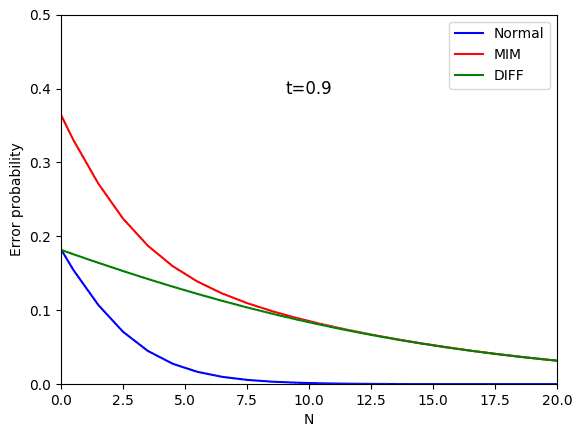
It looks like that my plot is not same with the original one in terms N=0 of Pe^MIM (red line) and differences between two error probabilities (green line). The problem is the calculation for error probability under MIM attack was not given.
I hope that anyone may help me to solve this problem.
Thank you.
The first equation is the error probability of authentication in normal operation:
cond equation is the error probability of authentication under MIM attack:
The error probability of authentication in normal operation can be calculated by:
Supposedly, the graph (original) will be shown like this:
y-axis: error probability
x-axis: N
Pe^normal = blue lines
Pe^MIM = red lines
Differences between two error probabilities (Pe^MIM - Pe^normal)= green lines
I tried to code it into Python and this is my full codes:
Python:
import matplotlib.pyplot as plt
import math
import numpy as np
from scipy.special import iv,modstruve
x=np.arange(-0.5,21,1)
x = np.array(x)
t = 0.9
pe_normal = (np.exp(t*x/2)*(iv(0, t*x/2) - modstruve(0,t*x/2))-1)/(np.exp(t*x)-1)
pe_diff = (np.exp((1-t**2)*x/2)*(iv(0, (1-t**2)*x/2) - modstruve(0,(1-t**2)*x/2))-1)/(np.exp((1-t**2)*x)-1)
pe_mim= np.add(pe_normal,pe_diff)plt.plot(x, pe_normal, '-', color='blue', label='Normal')
plt.plot(x, pe_mim, '-', color='red', label='MIM')
plt.plot(x, pe_diff, '-', color='green', label='DIFF')
plt.xlabel('Mean photon number N')
plt.ylabel('Error probabiity')
plt.text(10, 0.4, 't=0.9', size=12, ha='center', va='center')
plt.ylim([0, 0.5])
plt.xlim([0, 20])
plt.legend()
plt.show()The graph produce from my code is:
It looks like that my plot is not same with the original one in terms N=0 of Pe^MIM (red line) and differences between two error probabilities (green line). The problem is the calculation for error probability under MIM attack was not given.
I hope that anyone may help me to solve this problem.
Thank you.
Attachments
-
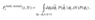 upload_2018-12-29_12-2-16.png2 KB · Views: 1,546
upload_2018-12-29_12-2-16.png2 KB · Views: 1,546 -
 upload_2018-12-29_12-2-48.png2.6 KB · Views: 1,320
upload_2018-12-29_12-2-48.png2.6 KB · Views: 1,320 -
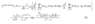 upload_2018-12-29_12-3-56.png5.7 KB · Views: 1,481
upload_2018-12-29_12-3-56.png5.7 KB · Views: 1,481 -
 upload_2018-12-29_12-4-42.png2.7 KB · Views: 1,444
upload_2018-12-29_12-4-42.png2.7 KB · Views: 1,444 -
 upload_2018-12-29_12-7-29.png6.3 KB · Views: 613
upload_2018-12-29_12-7-29.png6.3 KB · Views: 613 -
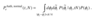 afNIG.png1.9 KB · Views: 607
afNIG.png1.9 KB · Views: 607 -
 upload_2018-12-29_14-29-55.png6 KB · Views: 1,383
upload_2018-12-29_14-29-55.png6 KB · Views: 1,383
Last edited:
