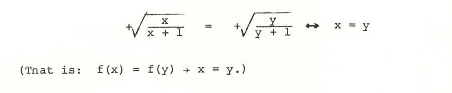To prove that a function has an inverse, it is essential to demonstrate that it is one-to-one, meaning each output corresponds to a unique input. The discussion emphasizes the importance of showing that if two outputs are equal, then their corresponding inputs must also be equal, which can be expressed mathematically. Graphing the function can help visualize this one-to-one relationship, but the core logic revolves around the if-then statement regarding inputs and outputs. The participants clarify that the basis for equating square roots is rooted in this logical structure rather than requiring additional proof. Ultimately, establishing that equal outputs imply equal inputs suffices to prove the function's invertibility.
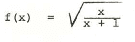 then to prove an inverse of this exists the following has been done to show that it is one to one
then to prove an inverse of this exists the following has been done to show that it is one to one