How to simplyfy a square root term? Phonon dispersion relati

[rwooduk]

I'm having trouble simplyfying this, I guess there's a trick but for the life of me can't remember what it is. Here is what I have so far:

$\omega ^{2} = f\left ( \frac{1}{m}+\frac{1}{M} \right )-f(( \frac{1}{m}+\frac{1}{M} \right ))^{2} - \frac{4q^{2} a^{2}}{mM})^{\frac{1}{2}}$

so I divide through by

$(\frac{1}{m}+\frac{1}{M})$

to give

$\frac{\omega ^{2}}{\frac{1}{m}+\frac{1}{M}} = f-f (\frac{4q^{2} a^{2}}{mM}(\frac{1}{m}+\frac{1}{M})^{-2})^{\frac{1}{2}}$

but now what? how would i simplyfy this further? here is the answer we have been given:

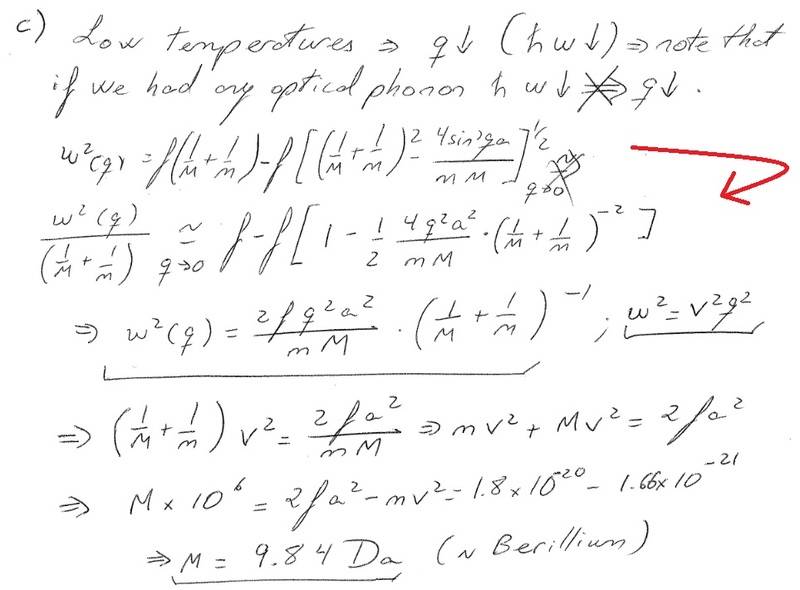
as you can see the square root has gone and there's a factor of 1/2 now inside the bracket, unclear of how he's simplyfied the square root term.

here's the complete question in line with forums rules:

thanks in advance for any help.

 

[rwooduk]

doesnt matter I am pretty sure he's used binomial theorem, mods please feel free to delete!