- #1
putrinh
- 1
- 0
How did you find PF?: Google search
I got a problem, how to calculate this formula from euler to imajiner? or how calculate this case?
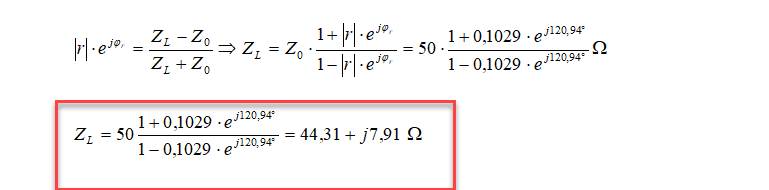
I got a problem, how to calculate this formula from euler to imajiner? or how calculate this case?