How to use Kirchhoff's voltage law on this circuit?

[NoahCygnus]

Homework Statement

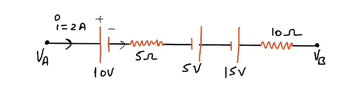
Calculate the potential at point O in the section of the circuit shown in the diagram.

Relevant Equations

$\Sigma\Delta V = 0$

In this circuit, I have to find the potential at point O. I tried using Kirchhoff's voltage law for the three open loops AOC, AOB and BOC to arrive at potential at O. According to my calculations the potential at O should be 0, but that is not the case according to the source. So I must be using Kirchhoff's voltage rule wrong. So can anyone guide me how to work this problem using KVL?

Here's my calculation:

Using KVL on AOC:

$V_1 +I_1R_1 +V_O -I_3R_3 = V_3$

Manipulating this equation to arrive at:

$I_1R_1 +V_O -I_3R_3 = V_3 - V_1$ (I)

KVL on AOB:

$V_1 +I_1R_1 +V_O - I_2R_2 = V_2$

Manipulation this to arrive at:

$I_1R_1 +V_O -I_2R_2 = V_2 - V_1$ (II)

KVL on BOC:

$V_2 +I_2R_2 + V_O -I_3R_3 = V_3$

Manipulating this equation to arrive at:

$I_2R_2 + V_O-I_3R_3 = V_3 - V_2$ (III)

Then using the three equations above to arrive at $V_O$

$III-(I-II)$
Do the math and we get $V_O=0$

But the answer in the textbook is $V_O=[V_1/R_1 +V_2/R_2 +V_3/R_3][1/R_1 +1/R_2 +1/R_3]^-1$.

What am I doing wrong?

 

[BvU]

well, for instance:$$V_1 +I_1R_1 +V_O -I_3R_3 = V_3$$ doesn't sound like KVL. Can you put KVL in words and check ?

$\$

 

[NoahCygnus]

well, for instance:$$V_1 +I_1R_1 +V_O -I_3R_3 = V_3$$ doesn't sound like KVL. Can you put KVL in words and check ?

$\$

"The algebraic sum of changes in potential around any 'closed path' of an electric circuit is zero."
I know the law mentions closed paths but hear me out. I have seen people use the law on open circuits treating the end points of the open path as closed.

I will take an example where I have seen people using KVL on open circuits:

Here we have to calculate potential difference between A and B,

I have seen people do this;

$$V_A - 10 - 2(5) + 5 +15-10(2) = V_B$$

I don't understand how they can do that, so I just followed the same thing on the circuit mentioned in my original problem.

 

[BvU]

I just followed the same thing

Fair enough. In that case, what would you think of e.g. $$
V_1 +I_1R_1 -I_3R_3 = V_3$$ i.e. without the $V_O$ ?

$\$

 

[NoahCygnus]

Homework Statement:: Calculate the potential at point O in the section of the circuit shown in the diagram.
Relevant Equations:: $\Sigma\Delta V = 0$

Using KVL on AOC:

$$V_1+I_1R_1+V_O−I_3R_3=V_3$$

But I did consider $V_O$ in the first equation. I am sure I didn't miss it.

 

[BvU]

I am sure I didn't miss it.

You certainly didn't. But you should have! Do you agree with $$\begin {align*} V_1 + i_1 R_1 &= V_O \tag{1}\\
V_2 + i_2 R_2 &= V_O \tag 2 \\
V_3 + i_3 R_3 &= V_O \tag 3 \qquad ?\end {align*}$$If so, then you should also agree with 1 + 3 yielding
$$\begin {align*} V_1 + i_1 R_1 -i_3R_3 &= V_3 \tag{1+3}\qquad !\qquad\quad\ \end {align*}$$


$\$

 

[Orodruin]

In other words, $V_O$ is not an emf in the circuit. It is just the value that the potential takes at O.

 

[NoahCygnus]

You certainly didn't. But you should have! Do you agree with $$\begin {align*} V_1 + i_1 R_1 &= V_O \tag{1}\\
V_2 + i_2 R_2 &= V_O \tag 2 \\
V_3 + i_3 R_3 &= V_O \tag 3 \qquad ?\end {align*}$$If so, then you should also agree with 1 + 3 yielding
$$\begin {align*} V_1 + i_1 R_1 -i_3R_3 &= V_3 \tag{1+3}\qquad !\qquad\quad\ \end {align*}$$


$\$

Oh yes, you used the loop law on AO, BO and CO instead of taking AOC, AOB and BOC like I did. I agree with that! But what's wrong with considering AOC, AOB, and BOC in my equations?

 

[NoahCygnus]

Oh yes, you used the loop law on AO, BO and CO instead of taking AOC, AOB and BOC like I did. I agree with that! But what's wrong with considering AOC, AOB, and BOC in my equations? How does that change anything?

 

[Orodruin]

Oh yes, you used the loop law on AO, BO and CO instead of taking AOC, AOB and BOC like I did. I agree with that! But what's wrong with considering AOC, AOB, and BOC in my equations?

Again, you used $V_O$ as an emf, not as just the potential value at O.

 

[NoahCygnus]

Again, you used $V_O$ as an emf, not as just the potential value at O.

Pardon my lack of knowledge, I know EMF is the potential of a cell when current is not drawn from it but I don't quite understand how I am using EMF of point O instead of its potential value.

 

[BvU]

No need to apologise ! We're all here (me too!) to make mistakes and have others help us to fix them somewhat.

taking AOC

If I take AOC I get
$$ \begin {align*} V_1 + i_1 R_1 -i_3R_3 -V_3 &= 0 \end {align*}
$$or, alternatively:
$$\begin {align*} V_1 -V_3 & = -i_1 R_1 +i_3R_3 \end {align*}
$$which, of course is all the same mathematically.

@Orodruin (and I) are trying to make clear to you that O is an intermediate point and that $V_O$ has no place in the loop equation.

$\$

 

[NoahCygnus]

No need to apologise ! We're all here (me too!) to make mistakes and have others help us to fix them somewhat.
If I take AOC I get
$$ \begin {align*} V_1 + i_1 R_1 -i_3R_3 -V_3 &= 0 \end {align*}
$$or, alternatively:
$$\begin {align*} V_1 -V_3 & = -i_1 R_1 +i_3R_3 \end {align*}
$$which, of course is all the same mathematically.

@Orodruin (and I) are trying to make clear to you that O is an intermediate point and that $V_O$ has no place in the loop equation.

$\$

Thank you. You are very kind. Reading your last statement and Orodruin's comment on how I am treating point O like it has an emf, I had a realization. There's just a wire at point O, there's no potential drop or gain there like in a resistor or a cell whose potential drop/gain we include in the equations. It's just a point on the wire, we don't include the potential at a point in the wire in the equations. Am I correct to assume that?

Also the equations where you used KVL on just AO, you included the term for $V_O$ because you considered it to be attached to a hidden cell not shown in the circuit with $V_A$ being the positive terminal and $V_O$ being the negative terminal. Is that assumption correct as well?

 

[BvU]

It's just a point on the wire, we don't include the potential at a point in the wire in the equations. Am I correct to assume that?

I think so, yes

Also the equations where you used KVL on just AO, you included the term for $V_O$ because you considered it to be attached to a hidden cell not shown in the circuit with $V_A$ being the positive terminal and $V_O$ being the negative terminal. Is that assumption correct as well?

It's an intermediate point. Three ways to get there and all three should end up at the same potential.

I don't think it is very useful to imagine an extra voltage source connected to that point (it should provide zero current anyway).
But if you do(*), O should be the positive terminal and ground the negative. (The same ground as the negative terminals of $V_1$ etc.)

Simple check: All $V_i$ equal. What is $V_O$ ?

(*) And that way you have 'upgraded' a three-point star to a four-point star.

$\$

 

[Orodruin]

It's just a point on the wire, we don't include the potential at a point in the wire in the equations

Exactly! Otherwise we could just add an arbitrary number of intermediate points and get a different result.

 

[NoahCygnus]

I think so, yesIt's an intermediate point. Three ways to get there and all three should end up at the same potential.

I don't think it is very useful to imagine an extra voltage source connected to that point (it should provide zero current anyway).
But if you do(*), O should be the positive terminal and ground the negative. (The same ground as the negative terminals of $V_1$ etc.)

Simple check: All $V_i$ equal. What is $V_O$ ?

(*) And that way you have 'upgraded' a three-point star to a four-point star.

$\$

Yes, O should be positive as conventional current goes from O to A. If I do imagine a voltage source connected to O, could you elaborate how why it should provide zero current?

 

[Steve4Physics]

On a related point, may I point out that the Post #1 diagram shows 3 currents leaving point O, violating Kirchoff's first law! Of course, that can be resolved if one or two of the current-values is/are meant to be negative.