Hydrostatic Fluid- Linearly Accelerating Slope

[AnnaJa]

Homework Statement

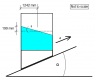
An open rectangular tank contains water up to about half of its depth. This tank accelerates at a=2.20 m/s$^{2}$ up a slope α (alpha), which causes the free water surface to form an angle θ (theta) with the original horizontal plane.
What is the α angle of the slope?

Homework Equations

p=ρh(g$\stackrel{+}{-}$a)
tanθ=$\stackrel{a}{g}$

The Attempt at a Solution

θ=tan$^{-1}($$\stackrel{199}{1242}$)=9.1°

angle between water surface and slope = γ

γ= α+θ

tanγ=($\stackrel{a}{g}$)

tanγ=($\stackrel{2.2}{9.81}$)

γ=12.64°

α=γ-θ=12.64-9.1=3.54°

I am not sure if this is the right approach?

Any help would be greatly appreciated.
Thank you, Anna

 

[KataKoniK]

Hello Anna,

Firstly, great job on using the appropriate equations and attempting to solve the problem. Your approach is mostly correct, but there are a few things that can be improved upon.

1. The angle θ that you calculated is incorrect. To find the angle between the water surface and the original horizontal plane, we need to use the inverse tangent function with the ratio of the opposite side (199) to the adjacent side (1242). So, θ = tan^-1(199/1242) = 9.1°.

2. The angle γ that you calculated is also incorrect. The angle between the slope and the original horizontal plane is not the same as the angle between the water surface and the slope. To find this angle, we can use the inverse tangent function with the ratio of the opposite side (a) to the adjacent side (g). So, γ = tan^-1(a/g) = tan^-1(2.2/9.81) = 12.64°.

3. Now, to find the angle α, we need to use the fact that the angle θ is formed by the slope and the original horizontal plane, and the angle γ is formed by the water surface and the slope. So, we can use the following equation: γ = α + θ. Substituting the values, we get α = γ - θ = 12.64° - 9.1° = 3.54°.

So, your final answer is correct! Good job. Just make sure to double check your calculations and try to understand the problem and the equations better. Keep up the good work!