blahblah8724
- 31
- 0
I don't understand this estimation lemma example :(
We are given the 'curve',
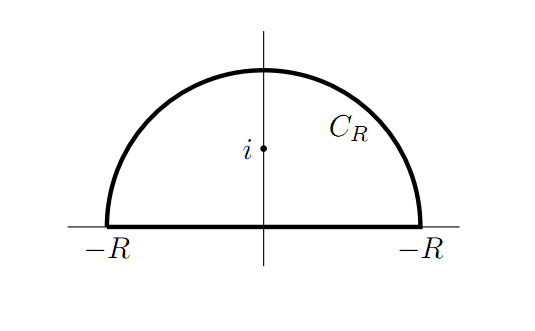
And part of the example is showing that the contour integral over the top semicircle C_R tends to zero.
Apparently we use the estimation lemma and the fact that, |z^2 +1| \geq |z|^2 - 1 to show,
\left| \int_{C_R} \frac{e^{iz}}{z^2 + 1} dz \right| \leq \int_0^\pi \frac{e^{-Rsin(t)}}{R^2 - 1} dt \leq \frac{2\pi R}{R^2 - 1} \to 0 as R \to \infty
However I don't understand the part where e^{iz} 'goes to' e^{-Rsin(t)}, is this some sort of parameterisation on the curve C_R?
Help would be much appreciated!
Thanks
We are given the 'curve',
And part of the example is showing that the contour integral over the top semicircle C_R tends to zero.
Apparently we use the estimation lemma and the fact that, |z^2 +1| \geq |z|^2 - 1 to show,
\left| \int_{C_R} \frac{e^{iz}}{z^2 + 1} dz \right| \leq \int_0^\pi \frac{e^{-Rsin(t)}}{R^2 - 1} dt \leq \frac{2\pi R}{R^2 - 1} \to 0 as R \to \infty
However I don't understand the part where e^{iz} 'goes to' e^{-Rsin(t)}, is this some sort of parameterisation on the curve C_R?
Help would be much appreciated!
Thanks