I need help generating a 2D representation of a curved plane

[OlarFin]

TL;DR

Need help creating a curved piece of wood for a project

When I was a freshman in college I never thought I'd use geometry...
BUT I WAS WRONG!
I purchased a laser engraving/cutting machine and my designs keep getting more complex. I have come to the end of what I can figure out or find on the web.

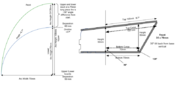
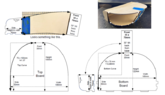
I am making a jewelry box for my wife that has a curved section that warps about 30 degrees as it curves. I need to calculate the arcs in 2 dimensions so that I can wrap the piece of wood to fit. In the first attachment is a photo of a piece of paper I manually tried to copy what the piece would look like.

Attached is:
1: Diagrams and images.
2: A more specific diagram that I hope shows what I'm trying to do.
(Please excuse the incorrect terms it's been 35 years since I last looked at this stuff - I'm flying by the seat of my pants.)

Any help is very appreciated!

 

[Mark44]

In the first attachment is a photo of a piece of paper I manually tried to copy what the piece would look like.

Cutting a piece of paper out as a template is the way to go. Doesn't that work for you? Can't you replicate in wood the same shape as the paper template?

It seems to me that the piece you're asking about should look something like this:

The curved parts are portions of circles or ellipses. Since the box is made from wood, it will need to be thin enough that you can steam it so as to be able to fit it into place.

BTW, in your thread title you mention a "curved plane." By definition, a plate is a flat surface.

 

[OlarFin]

Cutting a piece of paper out as a template is the way to go. Doesn't that work for you? Can't you replicate in wood the same shape as the paper template?

It seems to me that the piece you're asking about should look something like this:
View attachment 338429
The curved parts are portions of circles or ellipses. Since the box is made from wood, it will need to be thin enough that you can steam it so as to be able to fit it into place.

BTW, in your thread title you mention a "curved plane." By definition, a plate is a flat surface.

Ah, it would look like you indicated if there were no flexion of the piece.
The machine is so exact that I made a box with a lid that fits exactly since I provide the svg generated through Visio. The paper shape I made is close but I'm looking for exact.

 

[Mark44]

Ah, it would look like you indicated if there were no flexion of the piece.
The machine is so exact that I made a box with a lid that fits exactly since I provide the svg generated through Visio. The paper shape I made is close but I'm looking for exact.

The thinner the material, the better it will fit. I don't understand what you mean by "flexion of the piece."

 

[OlarFin]

The thinner the material, the better it will fit. I don't understand what you mean by "flexion of the piece."

Trying to create the piece by hand would look unfinished. In the first attachment it shows the two arcs that the piece needs to fill. Starts on the lower left and the top and bottom of the piece follows the top and bottom board. One curve is larger than the other. So the piece starts out and twists as it bends.
There has to be a mathematical way to do this.

Oof moth boards had the same arc. The piece I need would be a rectangle.

 

[Mark44]

So the piece starts out and twists as it bends.

Taking a closer look at your drawings, I'm not sure you can cut a piece out of flat material that will fit. If the top and bottom of the box were circles, I think you could cut a piece that would fit.

There has to be a mathematical way to do this.

As I said, I'm not sure there is, short of cutting pie-slice pieces out of the shape.

Oof moth boards had the same arc.

"Oof moth boards" -- ???

The piece I need would be a rectangle.

There's no way a rectangular shaped piece would fit, unless you're talking about the piece you start with, before making any cuts.