Ugnius
- 54
- 10
Hi! I have exam in couple of weeks , and now am looking for sources to learn about dynamic systems , chaotic systems and etc.
My main goal is to learn characteristics of such systems , learn about special points in dynamic plane.
For the most part we used to create dynamic system simulations like finding special points like saddles , spirals and centres , indentifying their stability. Now i'll need to do that in theory exam. I'll post some questions to give you better representation.
Examples:
How is dynamic chaos related to butterfly effect?
What are population dynamic models based on?
What are characteristics of chaotic dynamic system attractors?
On the picture below , you see a dynamic system plane.
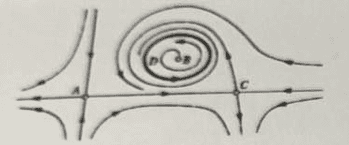
Is this system conservative or dissipative ? Is this system linear?
What special points do you see here , are they stable?
( On this last question , i'm especially lost , i've been looking to the literature given , but could find nothing similar , for me it looks like this is homoclinic bifirculation , but im not sure )
I don't want to make this post any longer, i'm very thankful in advance for anyone willing to guide me in a right way. Any source of information like books , threads or youtube videos will be helpful.
My main goal is to learn characteristics of such systems , learn about special points in dynamic plane.
For the most part we used to create dynamic system simulations like finding special points like saddles , spirals and centres , indentifying their stability. Now i'll need to do that in theory exam. I'll post some questions to give you better representation.
Examples:
How is dynamic chaos related to butterfly effect?
What are population dynamic models based on?
What are characteristics of chaotic dynamic system attractors?
On the picture below , you see a dynamic system plane.
Is this system conservative or dissipative ? Is this system linear?
What special points do you see here , are they stable?
( On this last question , i'm especially lost , i've been looking to the literature given , but could find nothing similar , for me it looks like this is homoclinic bifirculation , but im not sure )
I don't want to make this post any longer, i'm very thankful in advance for anyone willing to guide me in a right way. Any source of information like books , threads or youtube videos will be helpful.