Identifying gluon in Feynman diagram

[CAF123]

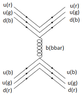
Sorry, I see I have been sloppy with how I wrote down my question - I don't mean to say that $\psi = (r b g)^T$ and $\bar \psi = (\bar r \bar b \bar g)$ are themselves colour singlets but the product $\bar \psi \psi$ (which defines my incoming state) is. So, with the above choices of $\psi$ and $\bar \psi$ I'm saying that $\bar \psi T^a \psi$ cannot produce a colour octet (that is, there exists no traceless T^a such that this expression is a linear combination of colour octet states). Is that correct?
Thanks!

 

[vanhees71]

No, it's already clear from the notation that $\bar{\psi} T^a \psi$ is not a singlet, because there's a free colour index $a$ in that expression. By definition of what's called the adjoint representation of SU(3) it transforms under SU(3) according to the adjoint representation. That's easy to see. The adjoint representation (which is 8-dimensional since you have 8 generators $T^a$) is defined by
$$T^{'a} = \hat{U}^{\dagger} T^a \hat{U}=U_{\text{ad}}^{ab} T^b,$$
where $\hat{U}$ are the matrices of the fundamental representation. The $8 \times 8$ matrices $U_{\text{ad}}^{ab}$ define the adjoint representation of SU(3). Now since
$$\psi'=\hat{U} \psi, \quad \bar{\psi}'=\bar{\psi} \hat{U}^{\dagger},$$
it's clear that $\bar{\psi} T^a \psi$ transforms according to the adjoint representation.

 

[CAF123]

Ok. I understand that a colour singlet to colour singlet state transition cannot happen with a single gluon based on arguments from group theory without using explicit representations of matrices. The vertex factor for such an amplitude gives a Tr T^a which is zero. But how to see the same result using explicit representations of Gell mann matrices? (I mean in terms of dealing with colour flow, dealing with explicit $\bar \psi$ and $\psi$ e.g)

 

[Vanadium 50]

(I mean in terms of dealing with colour flow,

You seem to be thinking of QCD elementary charges being "red", "green" and "blue", but otherwise mostly behaving like QED charge, Nothing good can come of this. In QED (or any U(1) theory), charge is a number. In QCD (or any SU(2) or SU(3) theory) charge is a matrix, and operations on matrices are not the same as for numbers. Intuition based on QCD being a numeric charge, or three kinds of numeric charge will lead you to wrong answers.

 

[CAF123]

Okay thanks - I think one of the things that has caused me a bit of confusion is the diagram as shown on P.254 of here:
http://www.hep.phy.cam.ac.uk/~thomson/partIIIparticles/handouts/Handout_8_2011.pdf

- it shows a picture of the mediation of a rrbar gluon and explicit colour flows on the diagrams. From the discussions in this thread, would you then say these sorts of diagrams are to be taken with a pinch of salt?

Also @Orodruin - about the 8x8 = 1 + ... comment, does it just mean that the appearance of 1 in the 8x8 decomposition allows for a colour singlet exchange to be mediated through two gluons?

 

[Vanadium 50]

then say these sorts of diagrams are to be taken with a pinch of salt?

They need to be understood as heuristic aids. He points out a few slides earlier that physical states are color singlets, and everything needs to be taken in that context.

 

[Orodruin]

A similar effect occurs in $\pi_0$ decays. A priori, you can draw a Feynman diagram with the quarks of the pion and an electron positron pair with the exchange of a single photon. At face value, this decay would be of the same order in the coupling constant as the dominating $\pi_0 \to 2\gamma$. However, the quark spins in the bound pion state are arranged in a way that does not match the intermediate photon state and the branching ratio of $\pi_0 \to e^+ e^-$ is $6.5\cdot 10^{-8}$.

 

[CAF123]

@Orodruin
Was this a reply intended for another thread?

 

[Orodruin]

@Orodruin
Was this a reply intended for another thread?

No. The idea is the same. You can draw a valid Feynman diagram but the symmetry of the in state makes it equal to zero.

 

[CAF123]

Ok. So the essence of this all is that the single exchange is mediation of a octet (8) between two singlet states and the double gluon exchange is the mediation of an 8x8 = 1 + ... The latter includes a singlet in its decomposition so allows for a colour singlet exchange to happen between the two colour singlet states. Yes?

 

[Vanadium 50]

The latter includes a singlet in its decomposition so allows for a colour singlet exchange to happen between the two colour singlet states. Yes?

Right.

And 8x8 = 1 + 8 + 8 + 10 +10bar + 27

 

[CAF123]

Right.

And 8x8 = 1 + 8 + 8 + 10 +10bar + 27

Ok thanks, just a quick aside, how does one interpret, say, the irrep 10 or 27 in this decomposition? (e.g 1 is mediation of colourless exchange, I suppose 8 is a colourful exchange )

I guess its analogous to 3x3x3 = 1+8+8+10 in which the 3x3x3 could be in a state transforming under the baryon (bound state) decuplet (10) representation of SU(3) - but 8x8 is not a bound state so what is the corresponding interpretation of its irreps?

 

[Vanadium 50]

This is color. Baryons are colorless.

 

[CAF123]

Yup so in this case the decomposition of 3x3x3 was with respect to approximate SU(3) flavour. But any such state in this decomposition would transform in the 1 of SU(3) colour.

So for 8x8 (tensor product of two SU(3) colour octet irreps) we get 1 + ... as you mentioned. The 1 and the 8 appearing in this decomposition has a clear interpretation to me (the 1 meaning the exchange of a colour singlet, the 8 meaning an octet) but what does the 10 , 10bar and 27 intuitively mean?

 

[Vanadium 50]

has a clear interpretation to me (the 1 meaning the exchange of a colour singlet, the 8 meaning an octet) but what does the 10 , 10bar and 27 intuitively mean

I have no idea what your intuition is. I could say "a decuplet is like an octet only there are ten elements instead of eight", but you already know that. I don't know what else to say.

 

[CAF123]

What I mean is, 1 and 8 have the interpretation to mean colour singlet and colour octet exchange... What do the 10 and 27 physically mean?
Thanks!

 

[Vanadium 50]

What do the 10 and 27 physically mean?

Color decuplet and color 27-plet. (Dodekaseptaplet?)

 

[CAF123]

Color decuplet and color 27-plet. (Dodekaseptaplet?)

:P hehe but can you say anything about what the exchange of e.g a colour decuplet actually means?

 

[Orodruin]

Color decuplet and color 27-plet. (Dodekaseptaplet?)

"Septenvigintuple" according to Wikipedia

:P hehe but can you say anything about what the exchange of e.g a colour decuplet actually means?

Yes, the intermediate state transforms as a decuplet under SU(3) gauge transformations. Just as a singlet does not transform and an octet transforms as an octet. I do not understand what deeper physical meaning you are trying to find that you find in the singlet and octet cases that you do not find in the decuplet and septenvigintuple cases.

 

[vanhees71]

I think to get an intuitive idea about the SU(3), it's better to study flavor symmetry in hadron physics, Gell-Mann's "eightfold way". Then it becomes clear that groups describe ordering schemes. In this case you order the hadrons according to their flavor structure:

https://en.wikipedia.org/wiki/Eightfold_Way_(physics)

A classic about group theory in this context of physics is

H. Lipkin, Lie groups for Pedestrians, North-Holland Publishing 1965

 

[Vanadium 50]

but can you say anything about what the exchange of e.g a colour decuplet actually means

I don't think I can. As we went through before, in SU(3) charges are matrices instead of numbers. This tells you which matrices.

 

[CAF123]

I do not understand what deeper physical meaning you are trying to find that you find in the singlet and octet cases that you do not find in the decuplet and septenvigintuple cases.

Just to the extent that 3 and 8 are the relevant representations through which the fields of QCD transform. We don't discuss the 10 or 27 representation when developing QCD so I just wondered what is the physical meanings of these representations in the product state 8x8. Does that perhaps clarify my question?

 

[Vanadium 50]

As far as we can tell, Nature has only picked singlets, triplets and octets for color representations of particles. In theory there could by 6's or 15's or 35's or... Just like the only elementary charges picked were 0, +/-1/3, +/- 2/3 and +/-1.

 

[CAF123]

Ok but what is the difference between a 8x8 configuration transforming in the 10 representation over one transforming in the 10bar or 27 rep?

There must be some physics there that is not encoded in say writing 8x8 = 1 + 8 + 35 + 10 + 3 + 7 or some other nonsensical sum of irreps. I realize that these decompositions are obtained by Young Tableuax but I am trying to understand what is the physical meaning of product states of the form 8x8 transforming in the 10 or 27 rep and the corresponding difference.

Thanks!

 

[CAF123]

A lot of the discussion in this thread was also brought up in the following video

1) At the beginning of it, it's said that a proton-proton scattering event cannot take place with the exchange of a single gluon. The argument is that an attempt to draw a Feynman diagram for this process results in colourful outgoing states with the exchange of a single octet. Now if I've understood this correctly, even though the diagram in the attachment is viable, when we sum over all possible quark colours the exchanged gluon would be equivalent to the ninth gluon, ie the one that transforms in the 1 of SU(3) colour and hence not physical.
(i.e I realize $b \bar b$ does not exist alone as one of the eight gluons (there is no linear combination of the eight orthogonal states to get a pure $b \bar b$ gluon state) but I could write the exchanged gluon as, say, $b \bar b - g \bar g$ which is a viable gluonic state and as far as I can see would not violate colour conservation in the above diagram. But if we change the quark colours that the gluon couples too, we would get a different gluon and the sum over all these for the full amplitude would amount to a non physical gluon).

2) I've seen in many sources that the colour factor $C_F$ for the amplitude between two colour singlet states mediated between a single gluon is given to be $4/3$. It is then said this results in an interaction potential between two singlets to be $-4/3 r^{-1}$. But if this process does not exist (as demonstrated e.g in the context of the proton proton scattering above) then what is the meaning of this non vanishing colour factor - should it not be identically zero since the process is not feasible?

See such remarks made in e.g, at the beginning of this video and at 55:30.

 

[Vanadium 50]

Well, that's 20 minutes of my life I am not going to get back.

I've seen in many sources that the colour factor CFC_F for the amplitude between two colour singlet states mediated between a single gluon is given to be 4/34/3.

That's not what he's written down on the board. He's written down that scattering between two quarks, and those are triplets.

I'm done. Sorry, but in the time it took me to wade through the video and discover that this is not what he said, I could have helped a half-dozen other people.

 

[CAF123]

Well, that's 20 minutes of my life I am not going to get back.
That's not what he's written down on the board. He's written down that scattering between two quarks, and those are triplets.

No, as I wrote at the bottom of my last post, the relevant part of the video is around 55:30. I mentioned this precisely so as to avoid needless watching of the whole video and to hone in on exactly where my questions arose. To be exact, the relevant part is 55:13 - 1hr:04, where he starts by considering the scattering of two colour singlets through exchange of a single gluon and the state of the incoming quark antiquark pair is the entangled colour singlet $\propto r \bar r + b \bar b + g \bar g$. He cranks through the colour factors and at about 1hr:04, notes the end result is just 4/3. I do not understand why this is non zero given that the process singlet -> singlet cannot be mediated through a single gluon.

 

[Vanadium 50]

If you do the frigging calculation with the correct frigging matrices you'll get the frigging right answer.

If you keep trying to take shortcuts by using r,g and b, or following random Youtube videos by obviously confused professors, you might not.

 

[CAF123]

If you do the frigging calculation with the correct frigging matrices you'll get the frigging right answer.

If you keep trying to take shortcuts by using r,g and b, or following random Youtube videos by obviously confused professors, you might not.

See the same result quoted at the bottom of this page (immediately preceding the summary) https://www.ippp.dur.ac.uk/~krauss/Lectures/QuarksLeptons/QCD/SimpleExample_1.html

and e.g in the exercises of 'An introduction to particle physics' by Mann - 'Show that 2 mesons in the colour singlet state $\frac{1}{\sqrt{3}} (r \bar r + g \bar g + b \bar b)$ experience a potential V=-4/3 1/r'

So I wouldn't say the professor is confused or that it is a random video. I am the one who is confused about this issue hence I ask on the forum.

Perhaps @Orodruin @vanhees71 can chip in again?
Thanks

 

[Vanadium 50]

See the same result quoted at the bottom of this page

That is the force between two triplets that are in the overall singlet state. It is not, repeat not, the force between two singlets.