Identifying gluon in Feynman diagram

[samalkhaiat]

'Show that 2 mesons in the colour singlet state $\frac{1}{\sqrt{3}} (r \bar r + g \bar g + b \bar b)$ experience a potential V=-4/3 1/r'

Not between two mesons. That is the short range potential between quark and anti-quark in a (colour singlet) meson, i.e., the QCD (colour) analogue of the attractive QED (electrostatic) potential. It is this potential that makes mesons the mesons we observe.
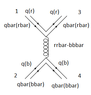
At short distances QCD is asymptotically free. This means that the q-q interaction gets weaker at short inter-quark distances, and at $r \sim 0.1 \mbox{fm}$ the lowest order (one-gluon exchange) diagrams dominate. So, it is not unreasonable to expect a Coulomb-like potential analogous to that arising from one-photon exchange in QED. Indeed, we can show that $$\langle q\bar{q}|V(r) |q\bar{q}\rangle_{\mbox{singlet}} = -\frac{4}{3} \frac{\alpha_{s}}{r} , \ \ \ r \sim 0.1 \mbox{fm} .$$ The factor $4/3$ arises from summing the colour factors of all possible lowest-order $q_{i}\bar{q}_{k} \to q_{j}\bar{q}_{l}$ partonic processes in the colour singlet meson. The colour factor for such partoinc processes arises when we calculate the Feynman amplitude $\mathcal{M}\left( q_{i}\bar{q}_{k} \to q_{j}\bar{q}_{l} \right)$. It is defined by $$C \left( q_{i}\bar{q}_{k} \to q_{j}\bar{q}_{l} \right) = \left( \frac{\lambda^{a}}{2}\right)_{ji} \left( \frac{\lambda^{a}}{2}\right)_{kl} .$$ Now, group theory comes to the rescue because of the following identity $$\left( \frac{\lambda^{a}}{2}\right)_{ji} \left( \frac{\lambda^{a}}{2}\right)_{kl} = \frac{1}{2} \left( \delta_{jl} \delta_{ik} - \frac{1}{3}\delta_{ji}\delta_{kl} \right) .$$ So, you find the following colour factors $$C(x\bar{x} \to x\bar{x}) = \frac{1}{3}, \ \ \ x = r, g, b ,$$ $$C(x\bar{x} \to y\bar{y}) = \frac{1}{2} , \ \ \ x \neq y ,$$ $$C(x\bar{y} \to x\bar{y}) = - \frac{1}{6} \ \ \ x \neq y .$$
So, “inside” the colour singlet meson, we have 3 partonic processes (diagrams) of the form $x\bar{x} \to x\bar{x}$ and 6 diagrams of the form $x\bar{x} \to y\bar{y}$. Thus $$C(q\bar{q} \to q\bar{q})_{\mbox{singlet}} = (\frac{1}{\sqrt{3}})^{2} \left( 3 \times (1/3) + 6 \times (1/2) \right) = \frac{4}{3} .$$
In similar but more complicated way, you can calculate the colour factor for two quarks exchanging a gluon within a colour-singlet Baryon $qqq$. However, one can deduce the value $C(qqq)_{[1]} = 2/3$ by simple group theory arguments.

 

[CAF123]

Thanks @samalkhaiat ! Few comments-

1)Why is it clear that this process describes the interaction between a q qbar pair in a single meson rather than the interaction between two mesons? I see, for example, that only the t channel exchange is considered and not a s channel. I am thinking that it is the s channel exchange that would describe an interaction between two mesons perhaps? Then the group theory factors are $\lambda^a_{ki} \lambda^a_{lj}$ and by summing over k and i (and also l and j) for colour singlet in initial (and final) state I get factors of $\text{Tr} \lambda_a$ which are identically zero (ie singlet -> singlet via one gluon is not permissible).

2) Where do the factors of $1/\sqrt{3}$ (used in the final equation display) come from in your analysis?

Thanks

 

[samalkhaiat]

1)Why is it clear that this process describes the interaction between a q qbar pair in a single meson rather than the interaction between two mesons?

1) You seem to over-look the most obvious facts and jump to strange and unfunded conclusions: the interaction potential between $e^{-}$ and $p^{+}$ in the Hydrogen atom is $- \frac{\alpha}{r}$. Do two Hydrogen atoms experience the same potential?
2) We can explain the heavy mesons spectrum very well by solving the Schrödinger equation for $q\bar{q}$ system with potential of the form $$V(r) = - \frac{4}{3} \frac{\alpha_{s}}{r} + b r + \mbox{spin-dependent potential} .$$

I am thinking that it is the s channel exchange that would describe an interaction between two mesons perhaps?

Perhaps you should tell me: why and how is that so? Can you show me how to write the meson-meson scattering amplitude in terms of their constituent quarks?

2) Where do the factors of $1/\sqrt{3}$ (used in the final equation display) come from in your analysis?

Look, the singlet state contains equal contributions from $r\bar{r}, \ g\bar{g}$ and $b\bar{b}$. Hence you only need to evaluate, say, the $r\bar{r}$ contribution and multiply this by 3: $$3 \cdot \frac{1}{\sqrt{3}} \left(r\bar{r} \right) \cdot \frac{1}{\sqrt{3}} \left(r\bar{r} + g\bar{g} + b\bar{b} \right) .$$ Now, the colour factors for $r\bar{r} \to r\bar{r} , \ r\bar{r} \to g\bar{g}$ and $r\bar{r} \to b\bar{b}$ are $C = \frac{1}{3} , \ \frac{1}{2}$ and $\frac{1}{2}$ respectively, giving you an overall colour factor $$C(q\bar{q} \in [1]) = \frac{4}{3} .$$

 

[CAF123]

Perhaps you should tell me: why and how is that so? Can you show me how to write the meson-meson scattering amplitude in terms of their constituent quarks?

1)Ok, indeed after reconsideration I see it cannot be. I suppose, however, the s channel exchange is then a viable diagram for the interaction between a q and q bar inside a single meson except that after imposition of the colour algebra its contribution simply vanishes so we are left with only the t channel exchange as discussed solely in the video too? (I say the s channel exchange is zero because it gives the factor $\text{Tr} \lambda^a$ outside the amplitude which is zero).

2) In the attachment of this post, I draw a diagram for one of the contributions to the naive process meson + meson - > meson + meson scattering through one gluon exchange. This diagram is consistent as far as I can see with all colour conservation and viable gluon mediation state. I call this a 'naive' process because it's well known that a singlet -> singlet cannot happen by exchange of one gluon. So it must be the case that by summing up all possible colour configurations for the quarks, it is then seen that the full amplitude for this process is zero. Is it the case that in this summation of all colour configurations, perhaps the exchanged gluon would be equivalent to the ninth (i.e unphysical SU(3) singlet) gluon and hence the process is not viable? (this is also alluded to in the video at the beginning for the pp -> pp scattering).

Thanks!