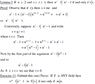If F is ANY field then (x^m-1)|(x^n-1) in F[x] if and only if m|n.

  • Thread starter taskforce123
  • Start date
  • Tags
    Field
In summary, the conversation is about proving the statement "If F is ANY field then (x^m-1)|(x^n-1) in F[x] if and only if m|n." The speaker has determined that m|n as long as n >= 2 and s >= r >= 1. However, they are now having trouble proving this for any field. They discuss the idea of using roots and linear factors, but realize this approach is not sufficient. They then mention that they have worked through a proof for the statement and attached it for reference. The question now is how to prove it for any field, and the suggestion is to go over the existing proof and make sure each step is justified in F(x).
  • #1
taskforce123
3
0
Hello. The question that I am having trouble with is the one found in the title. I will repeat it again here in the post.

"If F is ANY field then (x^m-1)|(x^n-1) in F[x] if and only if m|n."

I have determined that if m|n, then (x^m-1)|(x^n-1) as long as n >= 2 and s >= r >= 1. However, the part that I am now having trouble proving is that this statement holds for ANY field. I am not looking for an answer, but maybe a more precise definition of what I am trying to prove, and maybe the steps I need to take to prove it. Thank you very much in advance.
 
Physics news on Phys.org
  • #2
Here's an idea which doesn't work:

If [itex]x^n-1[/itex] divides [itex]x^m-1[/itex] then any linear factor of [itex]x^n-1[/itex] is a linear factor of [itex]x^m-1[/itex]. The linear factors correspond to the roots. So if [itex]x^n-1[/itex] divides [itex]x^m-1[/itex] then all roots of [itex]x^n-1[/itex] must be roots of [itex]x^m-1[/itex].

The is useless since a polynomial doesn't even need to have roots. Can you do something so that our approach will work?
 
  • #3
What are m,n? Naturals I assume
 
  • #4
Ok aassuming they are:

Perform division, paying attention to the form of the powers you get for the quotient
 
  • #5
I worked through the proof myself for the most part, but to make it easier to view, I attached the proof that was provided to us.

https://www.physicsforums.com/attachment.php?attachmentid=49748&stc=1&
d=1344716150

What I must prove now is that this holds for ANY field. This is where I get stuck. Basically, how would I go about proving that this statement holds for ANY field?
 

Attachments

  • Problem.png
    Problem.png
    12.1 KB · Views: 463
  • #6
Why don't you do the exact same things as in the lemma?? Only some notation will be different.
 
  • #7
It seems that what I need to do is prove that this works for ANY field. So would I need to do something extra with the already existing proof in order to solve the problem?
 
  • #8
taskforce123 said:
It seems that what I need to do is prove that this works for ANY field. So would I need to do something extra with the already existing proof in order to solve the problem?

Maybe. Go over the proof and see whether every step is justified in [itex]F(x)[/itex] (and why it is justified).
 

FAQ: If F is ANY field then (x^m-1)|(x^n-1) in F[x] if and only if m|n.

What is the significance of the statement "If F is ANY field then (x^m-1)|(x^n-1) in F[x] if and only if m|n?"

The statement is a fundamental theorem in abstract algebra that connects the divisibility of polynomials with the divisibility of their exponents. It states that in any field, if the polynomial x^m-1 is a factor of x^n-1, then m must divide n.

2. How is this theorem useful in mathematics?

This theorem has various applications in mathematics, including in the study of polynomial rings, abstract algebra, and number theory. It can also be used to prove other theorems and to solve problems involving polynomials.

3. Can you provide an example to illustrate this theorem?

One example is the polynomial x^6-1, which is a factor of x^12-1. This follows the theorem since 6 divides 12.

4. Does this theorem hold true for all fields?

Yes, this theorem holds true for all fields, including the real numbers, complex numbers, and finite fields.

5. Is there a converse to this theorem?

Yes, the converse of this theorem states that if m divides n, then (x^m-1) is a factor of (x^n-1) in any field. This means the theorem works in both directions.

Similar threads

Can Natural Numbers m and n Satisfy x + 1/m < y - 1/n?
Replies
22
Views
879
Problem 1-23 and 1-24 from Spivak's Calculus on Manifolds
Replies
6
Views
1K
Prove every subset of countable set is either finite or else countable
Replies
1
Views
1K
Integral of x^n using Reimann sums
Replies
4
Views
1K
Prove ##1 + a=s(a)=a+1## for ##a \in \mathbb{N}##
Replies
1
Views
995
Prove ##a \cdot 1 = a = 1 \cdot a## for ##a \in \mathbb{N}##
Replies
1
Views
1K
If ##|s_{n+1} - s_n| \lt 1/2^n##, then ##(s_n)## is a Cauchy sequence
Replies
9
Views
1K
Prove ##(a+b)\cdot c=a\cdot c+b\cdot c## using Peano postulates
Replies
3
Views
1K
Proof given ##x < y < z## and a twice differentiable function
Replies
8
Views
979
Prove that every subset ##B## of ##A=\{1,...,n\}## is finite
Replies
4
Views
932

Hot Threads

Recent Insights

Back
Top