Imaginary part of the dielectric function

[John Greger]

Hi everyone,

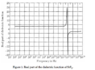
I was thinking about the complex part of the dielectric function. To my understanding there's good physical explanation of it. is a superimposed description of dispersion phenomena occurring at multiple frequencies.

Say I only have the real part such as the one below, and would like to get (approximately) the imaginary part. How could I obtain a plot of it, by just looking at the below figure? As using the Kramers-Kronig relation is rather tedious if you only want to get a sense of the behaviour.

I found the following statement: " the imaginary part leads to absorption loss if it is positive (in the above sign convention) and gain if it is negative." But I'm not sure how this would translate into a plot of the real part below?

Thanks in advance.

 

[jasonRF]

For a question marked "advanced" we require you to do a little more. Here is my hint: what would be a simple model of a (say) dielectric that could produce a real part that looks like this? There will be a few unknown parameters, but it should be pretty straightforward. Think physically (and classically) about bound electrons.

Jason

 

[John Greger]

For a question marked "advanced" we require you to do a little more. Here is my hint: what would be a simple model of a (say) dielectric that could produce a real part that looks like this? There will be a few unknown parameters, but it should be pretty straightforward. Think physically (and classically) about bound electrons.

Jason

Sorry, this isn't a hard question, but usually not encountered in undergrad courses.

I'm very much aware that the imaginary part of dielectric function is associated with the dissipation and thus it is responsible for the absorption. If an incoming photon can couple a filled state to an empty state, there will be absorption. If their a lot of photons which can couple these two states, their will be a big peak in the imaginary part of the dielectric function, because there will be more absorption. From the bandstructure it is possible to get by looking at every k-value and see which photon energthereheir are. Then counting for every photon energy how many times a certain photon energy can be used to absorb a photon leads to. If the bands a parallel, there will be a big peak in the imaginary part of the dielectric function. With the Kramer-Kronig relation the real part of the dielectric function can be calculated.

However, I was looking for a rule of thumb.

 

[jasonRF]

The rule of thumb is "derived" by using simple models, and that was what I was leading you to figure out. Here is the approach: model a bound electron position as a classical, damped harmonic oscillator driven by the electric field. This should give you a polarization that can then be used to derive the dielectric function. Your plot has a clear resonance-type feature in the real part, as will the simple model. But the model also gives you the right idea about what to expect from the imaginary part. You may also be able to figure it out physically: what do you think is happening at about $10^{13}$ Hz in your plot?

jason