Imaginary parts of amplitues (Schwartz QFT text)

[Lapidus]

From Schwartz http://isites.harvard.edu/fs/docs/icb.topic521209.files/QFT-Schwartz.pdf p. 257 or his qft book p. 455

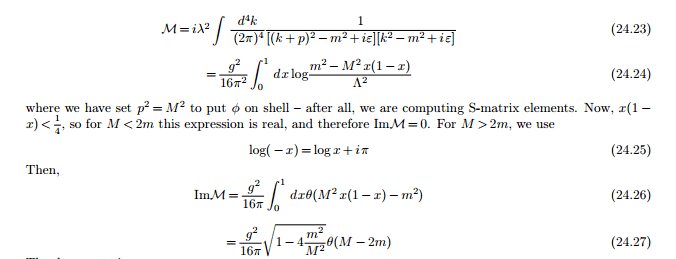
1. Why and how does the integral in (24.24) go imaginary, when M > 2m? Is it because the logarithms can not take negative real numbers, thus we have to switch to complex numbers?

2. (24.25) is the principal value equation, right?

3. How does (24.26) follow from what?! Is the little theta the theta step function?

4. How does (24.27) follow from (24.26)?! Taking the integral of the theta function gives us this square root term?

thanks for any hints and help

 

[mfb]

1. Why and how does the integral in (24.24) go imaginary, when M > 2m? Is it because the logarithms can not take negative real numbers, thus we have to switch to complex numbers?

2. (24.25) is the principal value equation, right?

3. How does (24.26) follow from what?! Is the little theta the theta step function?

Right.

4. How does (24.27) follow from (24.26)?! Taking the integral of the theta function gives us this square root term?

Integrating a step function just means you have to figure out where the steps are, in this case the integral starts at 0, then the function goes to 1 for a while and then goes to 0 again. The steps are at M²x(1-x) = m², solving that for x should give this expression for the difference between the x-values.

 

[vanhees71]

Note that the correct sign has to be negative. That's because you have to take the $\mathrm{i} \epsilon$ in the propagator (which gives the correct time-ordered operator which must be used in vacuum QFT). So the $m^2$ in the Feynman integral (2.24) should be taken as $m^2-\mathrm{i} \epsilon$, and then you have for the usual principle value of the logarithm $\ln (-x-\mathrm{i} \epsilon)=\ln(|x|)-\mathrm{i} \pi$, and you have to use the usual principle value, because the integral must be real for space-like four-momentum, i.e., for $p^2=M^2<0$.

Now to the integral for the imaginary part. Above threshold, $M^2>4 m^2$ the parabola $f(x)=M^2 x(1-x)-m^2$ is positive between its zeroes,
$$x_{1,2}=\frac{1}{2} (1 \pm \sqrt{1-\frac{4m^2}{M^2}}).$$
Since the square root is a monotonously growing frunction with $M \geq 2m$, it's easy to see that both roots are in the interval $[0,1]$, and thus you simply have
$$\int_0^1 \mathrm{d} x \Theta[M^2x(1-x)-m^2]=(x_1-x_2)=\sqrt{1-\frac{4m^2}{M^2}}.$$
This leads to the result (24.27) (which should be corrected for the subtle sign mistake mentioned above; note that it is in fact correct in the book on p. 455 Eq. (24.19)).