Impossible Op-Amp Circuit....Maybe

[Bullington]

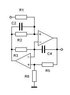
Could anyone verify if this is an impossible circuit, I put it in pSpice and it didn't work, I have no op-amps or voltage generators to build the circuit otherwise I would have built it. What do you all think, is it possible to find the transfer function of the far right op-amp? The schematic is attached

 

[NascentOxygen]

There is an absence of low-frequency (DC) feedback, so I expect the outputs will in short time be pegged at the supply rail.

 

[meBigGuy]

The 5 from the opamp to gnd is useless since OUT is 0 impedance.

There needs to be a resistance fron the center node to ground or spice won't converge (possibly PSPICE puts it there automagically. Try 100MegOhms tp ground.

No idea what "does not work" means. What was it supposed to do?

 

[Bullington]

Sorry, pSpice says there are two floating nodes, one at the node where C1 and R2 meet, and another where R3 and C2 meet. This is actually a circuit that was done in class, my professor came up with a solution for the transfer function; he said that the node where C1 meets R2 is not zero but it is an actual voltage.

 

[NascentOxygen]

The op-amp inverting inputs cannot be supplied with bias current, they are floating.

 

[LvW]

Did you create the circuit by yourself? I doubt if you have found this circuit in any documentation.
HOWEVER: This circuit is very similar to Antoniou`s very well known GIC circuit.
This GIC block plays a major role in active filter circuits (electronic (active) inductors, FDNR realizations, impedance transformation,...)

For example see here: http://images.google.de/imgres?imgu...d=0ahUKEwjbrbbvvvnLAhVDng8KHWrNAY4QMwgxKAowCg

 

[meBigGuy]

They are not opamps. They are ideal circuit elements, so there is no such thing as bias current.

Problem is that pspice will not simulate with floating nodes. For pspice, you need to add 100MegOhm resistors to ground on the floating nodes, other wise it can't find a quiescent solution to begin simulation.

 

[NascentOxygen]

They are not opamps.

They're not? What's that label beside each triangle in the schematic?

 

[Bullington]

I really wanted to get your opinions on this circuit without changing it, although I think if I add resistors it won't make much of a difference, the problem I see is the branch with C1 and R3 on it; this is an ideal op-amp so the voltage across the input terminals of an op-amp must be zero and C1 and R3 lay right in-between those terminals. Did I assume that correctly? Now that I have seen the GIC circuit, I do believe my professor actually meant to draw that one, or at least something similar to it.

 

[meBigGuy]

They're not? What's that label beside each triangle in the schematic?

I misspoke, kinda. They are ideal differential voltage sources, not "real" opamps. No output impedence, no bias current, no offset, infinite gain, etc etc.

Actually, using real models would solve his problem since those node would not be floating. Ironically that would change performance by more than the .000005% the resistors would add

 

[LvW]

Now that I have seen the GIC circuit, I do believe my professor actually meant to draw that one, or at least something similar to it.

Yes - that``s very probable. There are several alternatives within the GIC block for placing resistors and capacitors. There are two basic versions for active inductors and three versions for realizing an FDNR. More than that, active filter stages can also be realized directly. But in any case, it is absolutely necessary that each opamp has a negative DC feedback (DC path between output and inv. input), otherwise the circuit cannot work.

 

[meBigGuy]

But in any case, it is absolutely necessary that each opamp has a negative DC feedback (DC path between output and inv. input), otherwise the circuit cannot work.

Can you explain why in the context of a perfect amplifier with infinite input impedance, infinite gain, 0 offset, etc.

 

[LvW]

Can you explain why in the context of a perfect amplifier with infinite input impedance, infinite gain, 0 offset, etc.

What is the question? ("Why in the context of..." ?)

 

[meBigGuy]

Can you explain why? ( in the context of a perfect amplifier with infinite input impedance, infinite gain, 0 offset, etc.)

 

[LvW]

I am really sorry but I don`t know what I should explain?

 

[meBigGuy]

Where the DC content comes from that requires DC feedback path, for starters?

If there is no DC input, why is DC path needed?

 

[LvW]

OK - when I see an opamp symbol, immediately, I think of a real opamp and if the whole circuit will work as expected.
More than that, in the first post the questioner has mentioned that he couldn`t build the circuit because of some reasons.
Hence, my answer is related to real world conditions only. Was that your question?

 

[LvW]

Bullington, the attached image shows a GIC-based lowpass filter.
As you can see, it looks very similar to your circuit.
By the way - the necessary negative DC feedback for the most right opamp is established via R5, the other opamp, R3.

 

[Bullington]

So while I did try to build it, I still don't see how it is even theoretically possible; how could the branch where C1 and R3 are located do anything? Theoretically the voltage between the positive and negative inputs of an op amp are equal, so the current through C1 and R3 must be zero and if the current there is zero then the only place current can be measured is between the resistors R1 and R2 and the voltage out of the U2 op-amp is zero. Is this wrong?

 

[LvW]

Bullington, are you still speaking about "your" circuit ? Why do yu want to analyze a circuit that makes no sense?

 

[Bullington]

Well, has anyone actually confirmed it doesn't make sense on both a physical and theoretical scale? I have my reasons for it being a bad circuit but I wanted to see if you all agree.

 

[LvW]

Bullington, when I am asked to confirm if a certain circuit makes sense or not, at first I need to know what the purpose (the task) of the circuit is.
So - what is it?

 

[Bullington]

is it possible to find the the gain or transfer function?

 

[LvW]

Ys, here is the transfer function between input and output of the most right opamp.
The FINITE opamp gain values are E1 and E2, respectively. Good luck.

( + E1 C2 R2 R4) s

( + E1 C2 C1 R2 R3 R4) s^2

------------------------------------------------------------------------------

( + E2 C1 R2 R4 + E2 C1 R1 R4 + C1 R2 R4 + C1 R1 R4 + E2 E1 C2 R2 R4 + E2 E1 C2 R1 R4 + E1 C2 R2 R4 + E1 C2 R1 R4 + C2 R2 R4 + C2 R1 R4) s

( + E2 E1 C2 C1 R2 R3 R4 + E2 E1 C2 C1 R1 R3 R4 + E1 C2 C1 R2 R3 R4 + E1 C2 C1 R1 R3 R4 + C2 C1 R2 R3 R4 + C2 C1 R1 R3 R4 + C2 C1 R1 R2 R4) s^2

 

[Bullington]

Wow! How could that be if the voltage across C1 and R3 is zero? And, if the voltage across those components are not zero, then how? For an op amp the voltage across the positive and negative inputs are zero; so if a branch is connecting the two then that branch is zero, and if that branch has zero voltage then the current is zero; is this correct?

 

[LvW]

The voltage between the opamp inputs is zero for IDEAL opamps only. However, as I wrote, E1 and E2 are FINITE gain values. I have used a symbolic analyzer which, of course, does not accept infinite values.
But if you like you can set these values to infinite and look what happens.

 

[NascentOxygen]

I have my reasons for it being a bad circuit

What does this mean?? [emoji79]

 

[jim hardy]

I submit
it's a sophistic rhetorical electronics riddle. And a control system exercise.

1. Absence of DC coupling assures it'll saturate.
2. Dueling opamps compete for control of same node.
3. Extraneous parts are thrown into confuse us.

Left pointing opamp call him Louie,
tries to hold his inverting input at zero, same as his noninverting input
because that's what opamp circuits do, hold inputs equal.

Right pointing opamp call him Ralph,
tries to raise his inverting input to same as his noninverting input
because that's what opamp circuits do .

But - Those two inverting inputs share a node.
So who will win control of that node?
I say Louie will win because he controls the noninverting input to Ralph.


I submit (what others have already said):
1. Build this with real opamps and it should go to a rail when C1 and C2 charge because of input offsets
2. Build this with real opamps and it'll probably oscillate as fast as the opamps can slew.
3. R4 does nothing. C1 and R3 only reduce Ralph's gain.
So i removed all three parts to simplify thinking. See picture...

Toning down Ralph's gain via R3 and C1 just might keep it stable long enough to watch it integrate to a rail.
I'd like to see somebody breadboard it with 5 meg resistors and 5uf capacitors.

What do you guys think ?

Ralph has some transfer function
If we call that G, and call Louie a negative feedback H of 1,

what's closed loop response G/(GH+1) ?

 

[jim hardy]

Whew - Took me 5 edits to get that wording right...

 

[davenn]

Whew - Took me 5 edits to get that wording right...

awesome effort, you blinded me with such a brilliant insight :)


D

 

[LvW]

What do you guys think ?

Well, for REAL opamps I don`t think that a transfer function can be given because there will be no operational point within the linear region of the opamps.
Therefore, the node "NODE" will never be at zero volts (this would be valid for working negative DC feedback for both opamps only).
Instead, I think that both opamps will go into saturation.

 

[jim hardy]

Well, for REAL opamps I don`t think that a transfer function can be given because there will be no operational point within the linear region of the opamps.
Therefore, the node "NODE" will never be at zero volts

Whenever there's capacitors that can hold charge one must specify among his initial conditions their state of charge. Remember "Constant of Integration" from first semester calculus ?

So, start the thought experiment with initial condition of zero volts everywhere including isolated NODE , and ideal opamps.
Any change in voltage at Ralph's +input will propagate through Ralph, through C2 to Node
which will cause Louie to immediately reach around and undo that change .
So Ralph is held at zero output by Louie, the feedback element. Gain of circuit is zero.

It's a little easier to see if you remove R2, all he does is halve Vt.

Ralph is a unity gain voltage follower , transfer function of 1
Louie is feedback with gain and transfer function of ∞
closed loop transfer function G/(1+GH) is 1/(1+1X∞) = 0

I'd call the circuit a "Frustrated Voltage Follower ".
@Bullington ---- See what Professor thinks ?

but i agree it wouldn't work with real parts.

old jim