SUMMARY
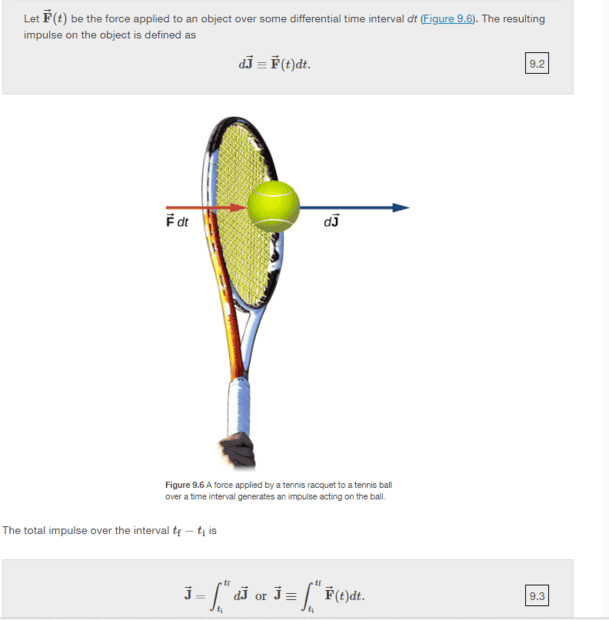
The discussion centers on the integration of impulse over time in the context of physics, specifically regarding the impulse experienced by a tennis racket when hitting a tennis ball. Participants clarify that integrating impulse from time intervals ##t_i## to ##t_f## is appropriate because impulse is a function of time, represented as ##\vec J(t)##. The alternative suggestion of integrating from impulse values ##j_i## to ##j_f## is deemed less suitable unless those values are known. The conversation emphasizes the importance of correctly identifying the variables involved in the integration process.
PREREQUISITES
- Understanding of impulse and its relation to force and time
- Familiarity with calculus, specifically integration techniques
- Knowledge of physics concepts related to motion and forces
- Ability to interpret mathematical notation in physics
NEXT STEPS
- Study the relationship between force and impulse in classical mechanics
- Learn about the mathematical principles of integration in physics
- Explore the concept of cumulative impulse and its applications
- Investigate the implications of omitting variable dependencies in mathematical expressions
USEFUL FOR
Students of physics, educators teaching mechanics, and anyone interested in the mathematical modeling of physical interactions, particularly in sports science.