Index of Refraction Through a Cylindrical Tube

[C. C.]

Hello All,
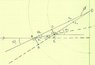
I would like to start learning how to ray trace but the tracing through a tube with a thickness of t has got me stumped. If I have an n1 (outside tube), n2 (Tube), and n3 (inside tube). n1≠n2≠n3. Knowing Θ1 (the angle of incidence in relation to the normal), I can calculate Θ2 from Snell's Law. The problem is that I am not sure as to how to calculate Θ3 (At the interface of the tube to the Inside of the tube). I am pretty sure I need to solve for Θ3 in relation to Θ2. I tried to approach the problem by trying to find the arclengths from the center of the tube, but I could not solve it from that method. Does anybody have some experience in this to point me in the right direction.

I have attached a drawing since my explanation is not very clear. The drawing is not to scale. r2 refers to the radius of the outer circle and r1 refers to the radius of the inner circle.

Thanks for any help!

 

[mfb]

In general, that is the intersection of a line and a circle, and trigonometry should work.
Depending on the numbers, it might be possible to use some approximations (especially if r1 and r2 are not too different).

 

[C. C.]

Thanks for the response. Given that the difference between r1 and r2 cannot be ignored, I get that the slope of line AC is the tan(θ1-θ2) [Taking point A as the origin]. The problem I run into is how would I determine the length of AC, or would that even matter?

 

[mfb]

I would solve that in a system where r2 is along one of the axes (and the center is the center of the coordinate system), the second part is tricky enough. Can you set up equations for the line and the triangle?

 

[C. C.]

Thanks, I think I correctly solved the value of the angle. I calculated AC then calculated the angle OCA. I was then able to figure it out. Appreciate the help.