Induced voltage in a coil in a three phase permanent magnet axial flux generator

[Frederik]

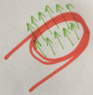
I am currently designing a three phase permanent magnet axial flux generator, but have a question regarding the voltage induced in the copper coils. Faraday's law defines this voltage as the number of turns in the coil, times the change in flux (external magnetic field times area of coil) over the change in time. As i tried to illustrate in this sketch:

However in my generator (and to my knowledge, in most others), the interaction between the coils and the flux is a bit different. I am not sure how to define the area in my case, as the source of flux is not passing through the entire coil, but instead parallel to it. The sketch below describes the basic principle of my generator:

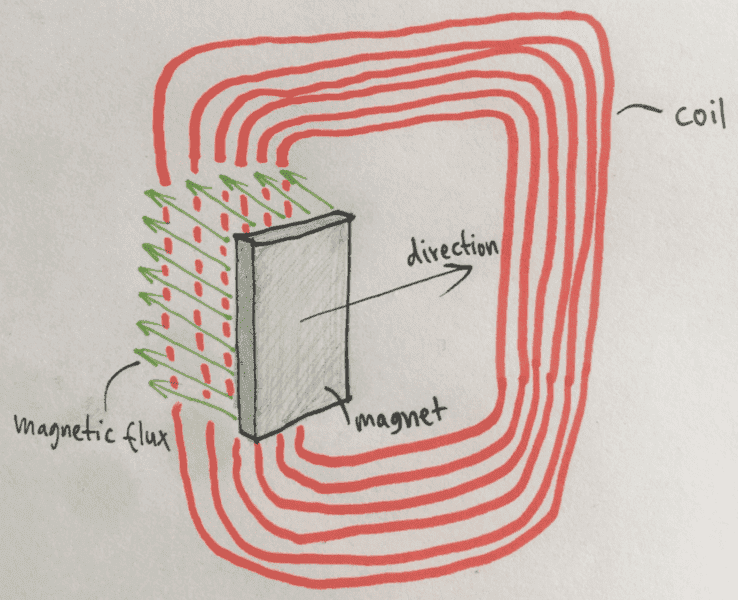
I just assumed that the area is that of the coil section affected by the magnet, instead of the total coil area, as shown here:

My question is, if the above assumption is correct?

Any help is greatly appreciated

 

[Borek]

The general form of the Faraday's law has a differential form - which in turn means you usually need calculus to find the voltage. The non-differential version that you refer to is a very specific case, quite easy to apply when it works, but outside of its applicability it fails miserably (as you have just realized).

 

[cabraham]

Any text on machines covers this in detail. Learning the details of generator operation is too much for posting here.

Claude
EE
PhD student

 

[jim hardy]

What counts is the amount of flux encircled by the coil. That's why your statement above says

number of turns in the coil, times the change in flux

Note it says flux not flux density.

Flux is measured in Webers.

(external magnetic field times area of coil)

That infers you are thinking of the magnetic field in terms of flux density , which is Teslas and usually represented by uppercase B,
instead of flux which is Webers usually represented by Greek letter "phi" Φ.
A Tesla is one Weber per square meter.
That's why you multiply by area, to change from Teslas that are present both inside and outside your coil to Webers that are encircled by it.

Think in Webers and your conundrum should disappear.

I just assumed that the area is that of the coil section affected by the magnet, instead of the total coil area, as shown here:

Nope. It's however many Webers the coil encircles. In your second picture with magnet smaller than coil you'll very soon encircle all the Webers, as in your first picture.

Being aware of that distinction should help you digest whatever textbook you consult.
B is not Φ so pay close attention to which symbol is in the author's formula.

old jim

 

[SHAURYE MAHAJAN]

How would you calculate the alternating current induced in the coils?