Jairo Rojas
- 17
- 0
Homework Statement
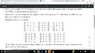
Attached is the problem
Homework Equations
The Attempt at a Solution
The trick to solve this problem is that when we assume that it is true for a 2^n x 2^n matrix and then we expand this matrix with 1's to a 2^n+1 x 2^n+1, we can divide the resulting matrix into 4 submatrices of 2^n x 2^n. 1 matrix will be crossed out already but the other 3 will have just 1 entries. To apply the inductive step on the 3 left matrices, we just perform an L transformation on the corner of the solved sub matrix. Now every left submatrix will have a 0. Therefore, they can be crossed by inductive hypothesis. My problem is that I don't know how to state formally that we can cross that specific L.