Inserting a conductor in a parallel-plate capacitor

[Joshua Benabou]

Consider a parallel plate capacitor formed by two plates of length $L$ and width $d$, separated by a distance $e$. There is a vacuum in between the plates. Let's note the capacitance of this arrangement $C_0$.

I insert a conducting plate of length $l=L/2$, with $D$, and thickness $e' <<e$. The position of the plate is measured by its $(x,y)$ coordinates, as shown below:

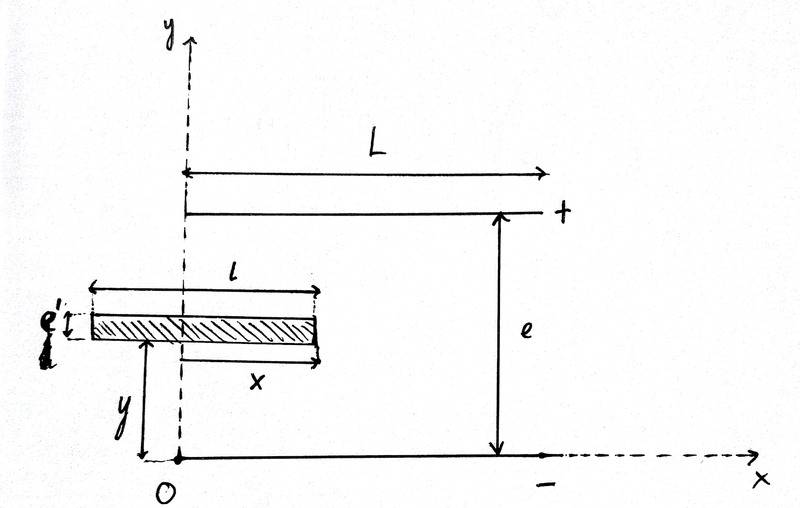
I would like to find the equivalent capacitance of this apparatus in terms of the distance $x$.

Of course if $x<0$, the conductor is not inserted at all so the capacitance remains unchanged, $C_0$.

Consider the case where the conductor is inserted partially, i.e $0<x<l$.

According to my notes, in this case the apparatus is equivalent to the arrangement of capacitors below:

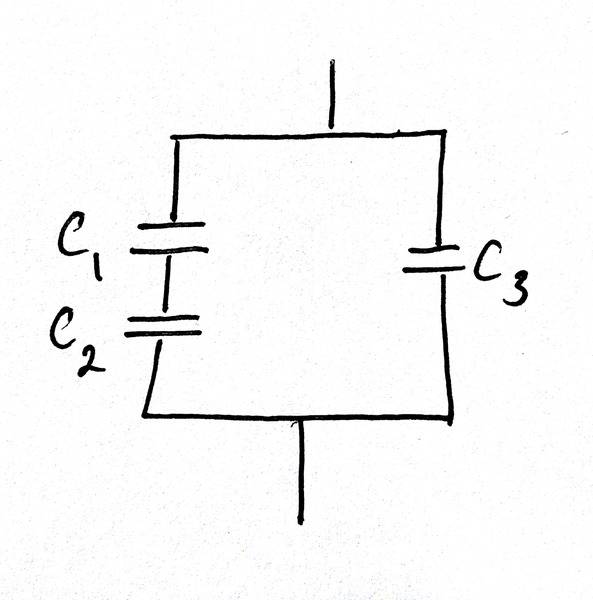
where

$C_1=\frac{\epsilon_0Dx}{e-y-e'}$

$C_2=\frac{\epsilon_0Dx}{y}$

$C_3=\frac{\epsilon_0D(L-x)}{e}$

**I do not understand why this configuration is equivalent to the arrangement of capacitors given above.**

I guess $C_1$ is the capacitor formed by the top plate and the conductor, $C_2$ the capacitor formed by the bottom plate and the conductor, and $C_3$ the capacitor formed by the conductor itself. However this leaves me confused as the capacitance for the conductor should then be:

$C_3=\frac{\epsilon_0Dx}{e}$

Finally, if we now consider the case where the conductor is fully inserted, i.e $l<x<L$, then apparently the capacitor arrangement changes completely and we now actually have four capacitors (2 in series, which are parallel with the other two). I don't understand why.

 

[BvU]

Hi,

As Sherlock Holmes would say: then the logical conclusion is that your guess was wrong ...

Look at $C_3$: is your guess logical if e.g. $x=0$ ?

 

[NFuller]

C3C3C_3 the capacitor formed by the conductor itself

As BvU has suggested, the issue is with your interpretation of $C_{3}$. The capacitor $C_{3}$ is considered to be the capacitance of the space to the right of the conductor, leading to the form of $C_{3}$ given in your notes.