Instability of a 1D material due to Fermi surface nesting

[tom8]

Consider the Lindhard response function:
\chi(\vec{q})=\int\frac{d\vec{k}}{(2\pi)^d}\frac{f_\vec{k}-f_{\vec{k}+\vec{q}}}{\epsilon_\vec{k}-\epsilon_{\vec{k}+\vec{q}}}
where $\vec{q}$ is the wavevector, $\epsilon$ is the free electron energy and $f$ is Fermi-Dirac distribution function. For 1D near $2k_F$, this reduces to:
\chi(q)=-e^2n(\epsilon_F)\ln\frac{q+2\vec{k}_F}{q-2\vec{k}_F}
where $n(\epsilon_\vec{F})$ is the density of states. Clearly $\chi(\vec{q})$ diverges near $\vec{q}=2\vec{k}_F$.

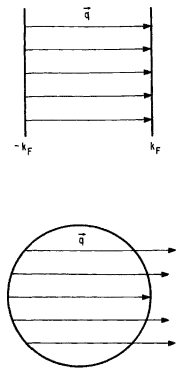
It is argued (see the picture below) that this divergence is due to Fermi surface nesting, which is represented by the arrows in the picture. What I do not understand is that why, in the 2D case, the arrows are restricted to be horizontal? I can still draw an arrow in any direction since this is a Fermi surface and all points have the same energy and are thus identical...

 

[DrDu]

Yes, but a vector is not one arrow but so to say all possible arrows which are parallel to each other. In 2d you will first integrate over all q with a given direction but different lengths and in a second step over all possible orientations. The first integral will not be as singular as in 1d due to the spherical Fermi surface. The second integration will not change this.

 

[tom8]

So you are saying that the divergence in 1D is more than in 2D per one nesting wavevector. If we will sum over all the possible nesting wave vectors in 2D, then so we do in 1D and it is the same.

But, if we look at the figure, the 1D case has two parallel lines. Anything other than a horizontal wavevector will be larger than $2 k_F$, while in 2D all orientations will still be $2 k_F$, so the argument above does not seem to hold.

 

[DrDu]

No, what I wanted to say was something different. There are no truly 1d materials. Rather what we mean in this context is a material whose Fermi surface consists of two almost parallel planes. You may think of a bunch of almost non interacting truly 1d materials which are hardly interacting.
Then one wavevector of length 2k_F will map each point from one surface to a point on the other.
In a 2 or 3d material, the corresponding Fermi surface will be more or less spherical, so independently of the wavevector, only isolated points will be mapped to isolated points.

 

[tom8]

...In a 2 or 3d material, the corresponding Fermi surface will be more or less spherical, so independently of the wavevector, only isolated points will be mapped to isolated points.

And how is this different? In 1D I can also say that individual points in one line are mapped to isolated points in the other. Collectively, these points constitute the line. In 2D the same is true. Sorry I can't just get it.

P.S. let's stick to ideal Fermi surface for the moment.

 

[DrDu]

You can't compare apples and pears. So 1d, 2d and 3d, are all actually 3 dimensional objects with the following ideal Fermi-surfaces: 1d=two planes, 2d=a cylinder, 3d=a sphere. Now in the integration over k space, the singularities of de denominator are of codimension 2( a plane) , 1(a line) , 0 (a point).

 

[tom8]

Oh I see. Now I understand your point, but (sorry) isn't the Fermi surface for 1D a line, 2D a circle and 3D a plane, how come now it is a plane for 1D and a cylinder for 2D?

 

[DrDu]

You can always consider a periodic array of non-interacting one dimensional objects to make up a 3d object. This is much more physical than considering a true 1d object. This is also what is implied in your graphics, as they represent the Fermi surface of a 1 d object as a line in a 2d space.

 

[tom8]

I see, thank you!