Biker
- 416
- 52
I studied statics but I thought I can figure out the dynamics part.
In a rectangular shape that is tipping, Usually we take the center of mass as an axis of rotation however the center of mass is accelerating with centripetal force so taking it would make the problem complex and we just take the tip that is touching the ground on the side that is moving to. Is this correct?
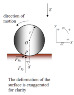
if we have a cylinder then both the center of mass and the point of contact are easy to analyze so both of them work. However I have a problem if we treat the problem realistically, The object isn't rigid so it will deform a bit so it touches the ground on an area not a line. I could analyze it around the center of mass but the book says that it rotates around the last line that is touching the ground on the side that the object is moving to. I don't see how it will give the same motion, The velocity don't seem to be equal. What is wrong?
In a rectangular shape that is tipping, Usually we take the center of mass as an axis of rotation however the center of mass is accelerating with centripetal force so taking it would make the problem complex and we just take the tip that is touching the ground on the side that is moving to. Is this correct?
if we have a cylinder then both the center of mass and the point of contact are easy to analyze so both of them work. However I have a problem if we treat the problem realistically, The object isn't rigid so it will deform a bit so it touches the ground on an area not a line. I could analyze it around the center of mass but the book says that it rotates around the last line that is touching the ground on the side that the object is moving to. I don't see how it will give the same motion, The velocity don't seem to be equal. What is wrong?