SUMMARY
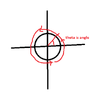
This discussion focuses on the calculation of integrals around a unit circle using polar coordinates. Participants clarify the distinction between line integrals and surface integrals, emphasizing that ds represents an infinitesimal arc length rather than a surface area. The correct parametrization involves using x = cos(t) and y = sin(t) with limits defined in radians. The conversation also highlights the importance of understanding the dimensionality of integrals, where the boundary of a manifold is one dimension lower than the manifold itself.
PREREQUISITES
- Understanding of polar coordinates and their application in integrals.
- Familiarity with line integrals and surface integrals in calculus.
- Knowledge of the concept of parametrization in multivariable calculus.
- Basic grasp of manifold theory and dimensionality in mathematics.
NEXT STEPS
- Study the application of the Divergence Theorem in vector calculus.
- Learn about the parametrization of curves and surfaces in higher dimensions.
- Explore the differences between line integrals and surface integrals in detail.
- Investigate the implications of dimensionality in manifold theory.
USEFUL FOR
Students and educators in calculus, mathematicians interested in integral theory, and anyone seeking to deepen their understanding of the relationships between different types of integrals and their applications in geometry.