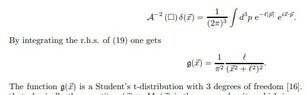Integral Calculation: Compute l/sqrt(x2+l2)

[PeteSampras]

Homework Statement

Help please with the integral of figure

Relevant Equations

In the description

I need compute the integral

$$(2\pi)^{-3} \int d^3p e^{-l|p|}e^{i \vec{x} \cdot \vec{p}}$$

The problem does not specified the limits of integration

The result is

$$\frac{1}{\pi^2} \frac{l}{\sqrt{\vec{x}^2+l^2}}$$I saw the references about t-Student and I had not achieved it.
I have tried to split the integral as

$$\int dp_x dp_y dp_z e^{-l\sqrt{p_x^2+p_y^2+p_z^2}} e^{ip_xx+ip_yy+ip_zz}$$
x2 without result.
Also I tried to insert a 2D dirac Delta and after integrate only in dp instead dp^2. Also without result

Could you help me to solve this integral?

 

[Orodruin]

Spherical coordinates.

 

[PeteSampras]

Spherical coordinates.

Do you say something like that

$\int_0^{2\pi}d\theta\int_0^\pi d\phi \int_0^\infty dp~p^2e^{-lp}e^{ipr\cos (\theta)}$

I also have intented without results

 

[Orodruin]

You are missing the $\sin\theta$ iof the volume element. (And a } that makes your LaTeX not render)

 

[Mark44]

(And a } that makes your LaTeX not render)

Fixed the LaTeX...

 

[pasmith]

Do you say something like that

$\int_0^{2\pi}d\theta\int_0^\pi d\phi \int_0^\infty dp~p^2e^{-lp}e^{ipr\cos (\theta)}$

I also have intented without results

You are missing the $\sin\theta$ iof the volume element. (And a } that makes your LaTeX not render)

In which case the limits of $\theta$ should be $[0, \pi]$ and the limits of $\phi$ should be $[0, 2\pi]$.