Opalg said:
True, but note that Wolfram defines the Heaviside function to take the value 1/2 at 0. The Wikipedia article gives the definition $$H(x) = \begin{cases}1&(x\geqslant0),\\ 0&(x<0).\end{cases}$$ That would lead to a delta function with all its weight concentrated on "one side of 0", so to speak.
I think the moral here is that it is necessary to pay attention to the definition used by the book or article that you are working from.
A concept I tried to explain in...
http://www.mathhelpboards.com/f13/never-ending-dispute-2060/#post9448
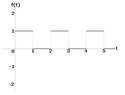
... is that there exist 'good' and 'bad' basic definitions, in the sense that a 'bad definition' leads, sooner or later, to contraddictions and logic failures and that doesn't happen with a 'good definition'. Now we have two different definitions of H(0), according to 'Monster Wolfram' is H(0)=1/2, according to 'Wiki" is H(0)=1... and we can't exclude that for someone else is H(0)=0... Very well!... which definition is 'good'?... an answer I think can come from the following example...Let consider the time function represented here...
https://www.physicsforums.com/attachments/486._xfImport
... that in term of Heaviside Step Function is written as...
$\displaystyle f(t) = \sum_{n=0}^{\infty} (-1)^{n}\ H(t-n)$ (1)
The Laplace Transform of (1) is computed in standard form as...$\displaystyle \mathcal{L} \{ f(t) \} = \frac{1}{s\ (1 + e^{- s})}$ (2)
Now we obtain f(t) performing the inverse Laplace Transform using the Bromwich Integral...$\displaystyle f(t) = \frac{1}{2\ \pi\ i}\ \int_{\gamma - i\ \infty}^{\gamma + i\ \infty} F(s)\ e^{s\ t}\ ds$ (3)
... where $\gamma$ is a constant that lies on the right respect to all the singularities of F(s). In this case the singularities of F(s) are $s=0$ and $s = (2 n + 1)\ \pi\ i$, i.e. all on the imaginary axis, so that any real $\gamma >0$ is 'good'.
The residue of F(s) in $s=0$ is...$\displaystyle r_{0} = \lim_{ s \rightarrow 0} s\ F(s)\ e^{s t} = \frac{1}{2}$ (4)... and the residue of F(s) in $s= (2 n + 1)\ \pi\ i$ is...$\displaystyle r_{n}= \lim_{ s \rightarrow (2 n + 1)\ \pi\ i} \{ s - (2 n + 1)\ \pi\ i \}\ F(s)\ e^{s t} = \frac{e^{(2 n + 1)\ \pi\ i\ t}}{(2 n + 1)\ \pi\ i} $ (5)
... so that the integral (3) supplies...
$\displaystyle f(t) = \frac{1}{2} + \sum_{n= -\infty}^{+ \infty} r_{n} = \frac{1}{2} + \frac{2}{\pi} \sum_{n=0}^{\infty} \frac {\sin (2n + 1)\ \pi\ t}{2n + 1}$ (6)
Of course the result is not a surprise, because the (6) is the Fourier Series of the (1). A 'little suprise' however is the fact that the (6) for t= n with n non negative integer converges to $\frac{1}{2}$ and that means that, comparing (1) and (6), we conclude that is $H(0)= \frac{1}{2}$... It seems that the 'good definition' is supplied by 'Monster Wolfram'...
Kind regards$\chi$ $\sigma$